In y= A sin ωt + A sin (ωt+(2π)/3) match the following table.
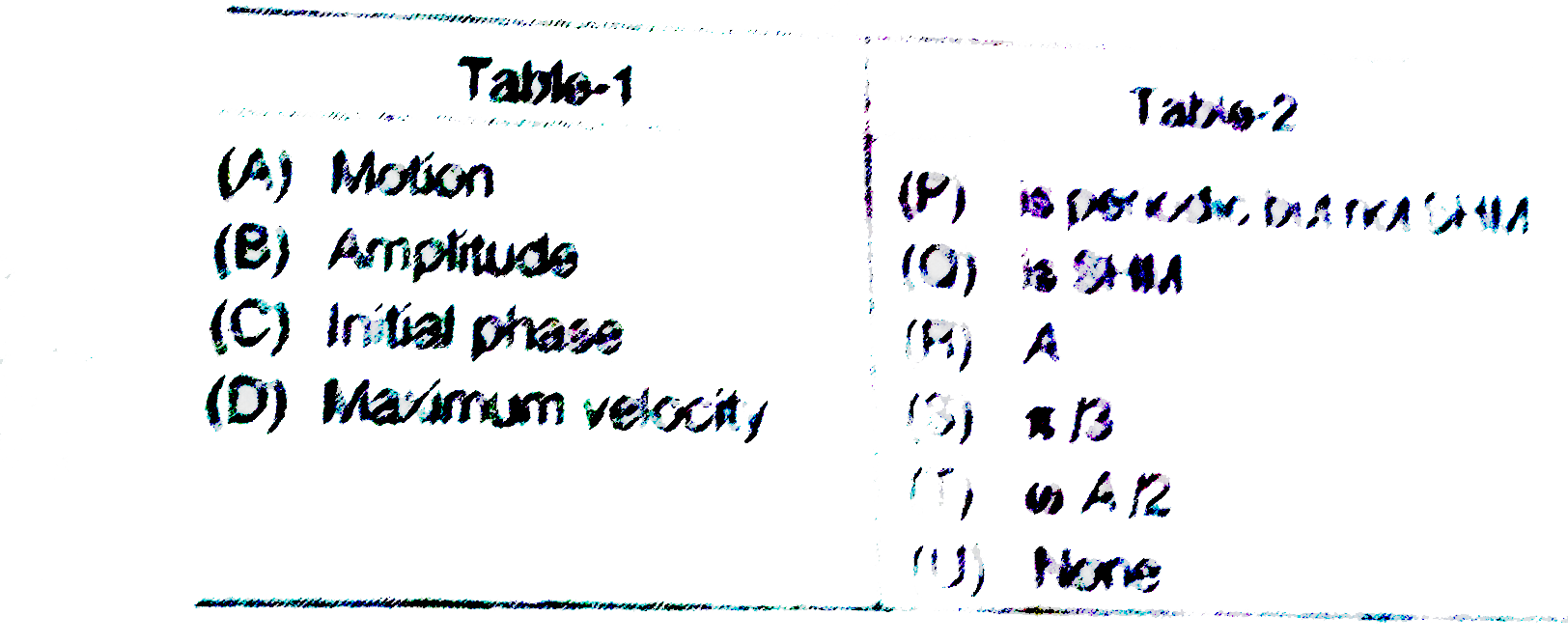
The correct Answer is:(A→q,B→r,C→s,D→u)
The given equation,
y=Asinωt+Asin(ωt+2π3) can also be written as.
y=2Asin(ωt+π3)cos(π3)=Asin(ωt+π3)
Now, we can see that this is SHM with amplitude A and initial phase π3.
Similar Questions
Consider the three waves z1,z2andz3 as
z1=Asin(kx−ωt)
z2=Asin(kx+ωt)
z3=Asin(ky−ωt)
Which of the following represents a standing wave?
View SolutionTwo partical AandB execute simple harmonic motion according to the equation y1=3sinωt and y2=4sin[ωt+(π/2)]+3sinωt. Find the phase difference between them.
View Solution
Knowledge Check
The equation of a body of mass m and performing a linear S.H.M is given by x=asinωt+bsin(ωt+π2). The total energy of the particle at any ins"tan"t is
A12mω2abB12mω2√a2+b2C12mω2(a2+b2)D12mω2√a2+b2The displacements of two interfering light waves are y1=2sinωt and y2=5sin(ωt+π3) the resultant amptitude is
A39cmB√39cmC7cmD√29cmA xandy co-ordinates of a particle are x=Asin(ωt)andy=Asin(ωt+π/2). Then, the motion of the particle is
 Acircular anticlockwiseBcircular clockwiseCelliptical clockwiseDrectilinear
Acircular anticlockwiseBcircular clockwiseCelliptical clockwiseDrectilinear
If two waves represented by y1=4sinωt and y2=3sin(ωt+π3)interfere at a point, the amplitude of the resulting wave will be about
View SolutionA particle is subjected to two mutually perendicular simple harmonic motion such that its x and y coordinates are given by :
x=2sinω & y=2sin(ωt+π2)
The path of the particle will be
View SolutionWhich two of the following waves are in the same phase?
y=Asin(kx−ωt)
y=Asin(kx−ωt+π)
y=Asin(kx−ωt+π/2)
y=Asin(kx−ωt+2π)
View SolutionTwo simple harmonic motions given by, x=asin(ωt+δ) and y=asin(ωt+δ+π2) act on a particle will be
View SolutionEquations y=2Acos2ωtandy=A(sinωt+√3cosωt) represent the motion of two particles.
View Solution