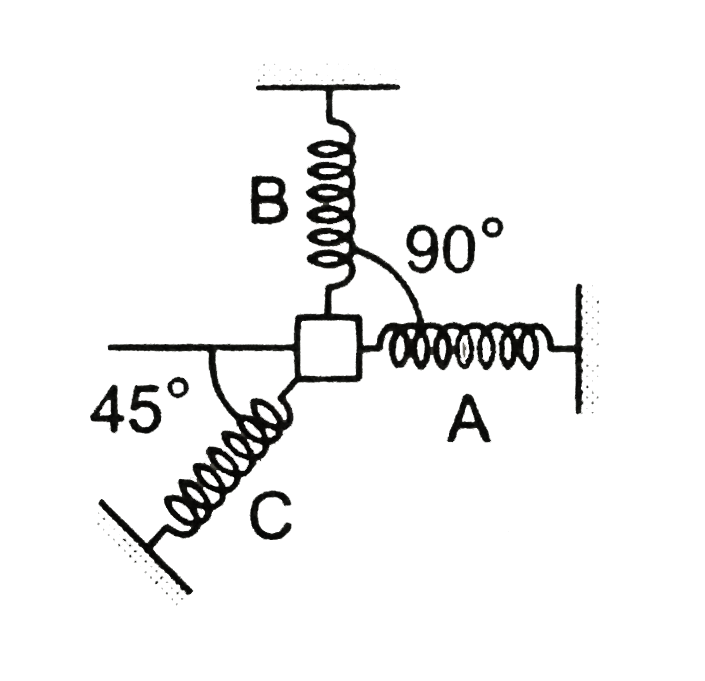
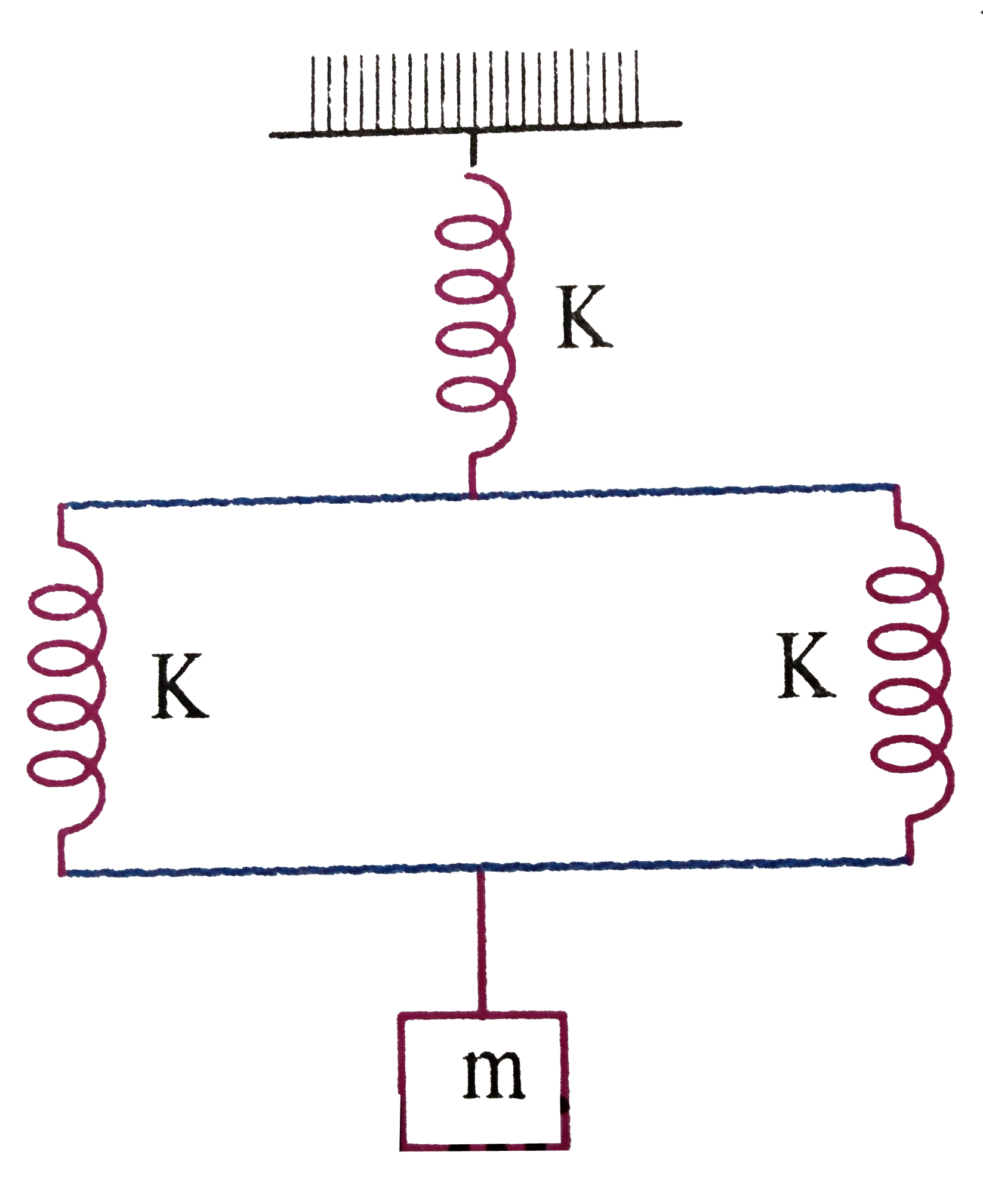
A particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is
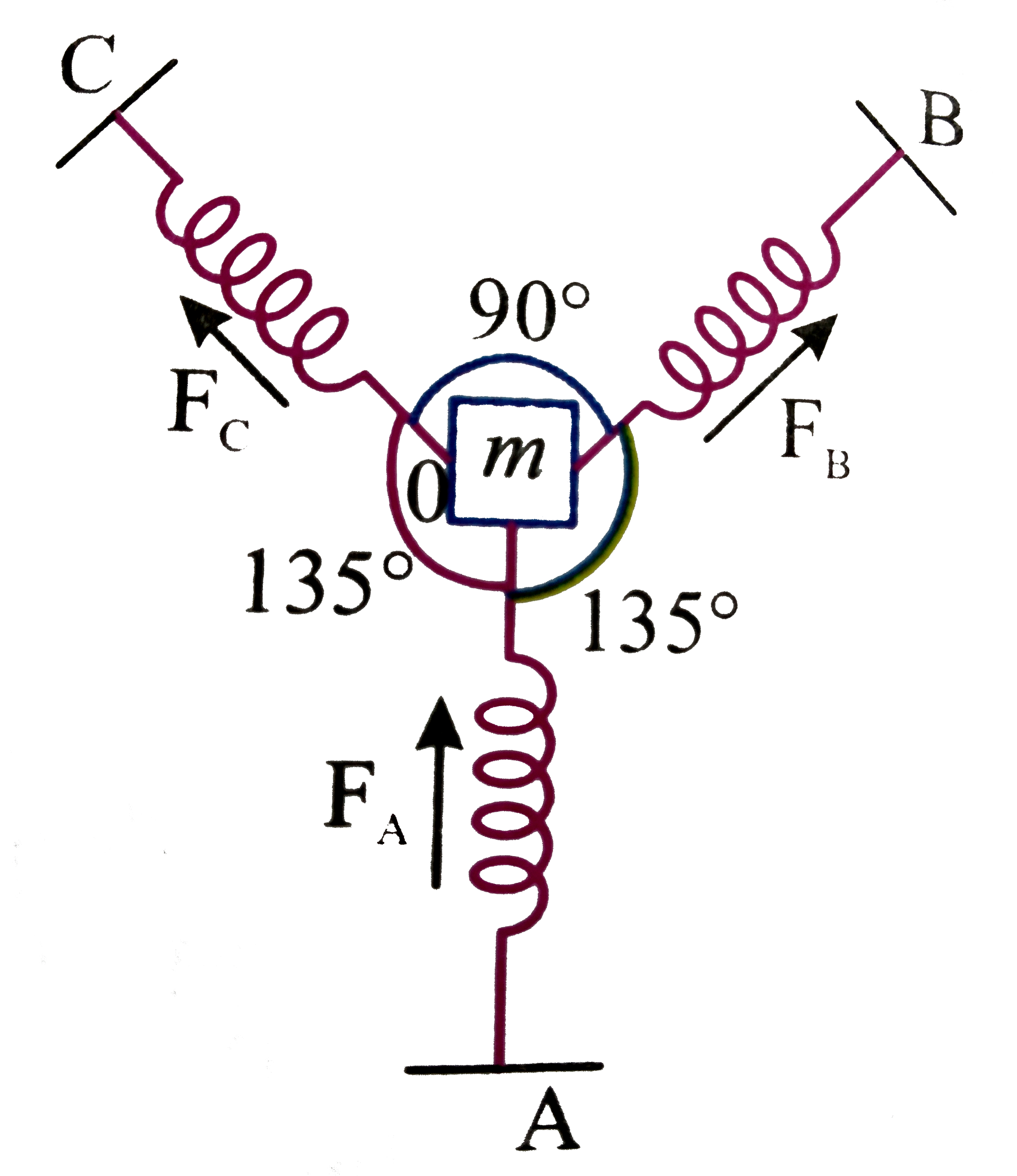
2π√2mk
2π√m2k
2π√mk
2π√m3k
The correct Answer is:B
(b)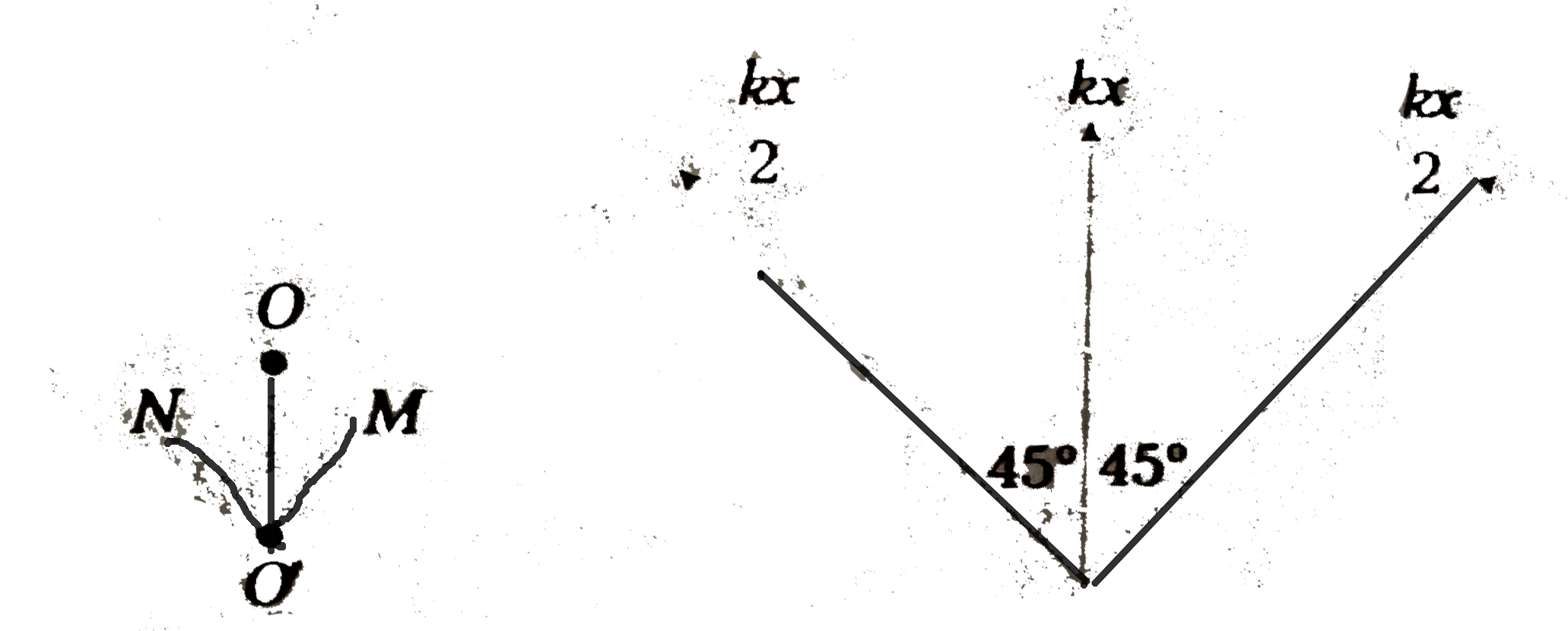
OO'=x(say)
Then O'M=O'N≈x√2
i.e., elongation in spring B and x/√2) , while compression in spring A is x.
Net restarting force
F=−[kx+2kx√2cos45∘]=−2kx
∴a=Fm=−2kmx
T=2π√∣∣xa∣∣=2π√m2k
Similar Questions
A particle of mass m is asttached to three springs A,B and C of equla force constants k as shown in figure. If the particle is pushed slightly against the spring C and released, find the time period of oscillastion.
 View Solution
View SolutionA particle of mass m is attached with three springs A,B and C of equal force constancts k as shown in figure. The particle is pushed slightly against the spring C and released. Find the time period of oscillation.
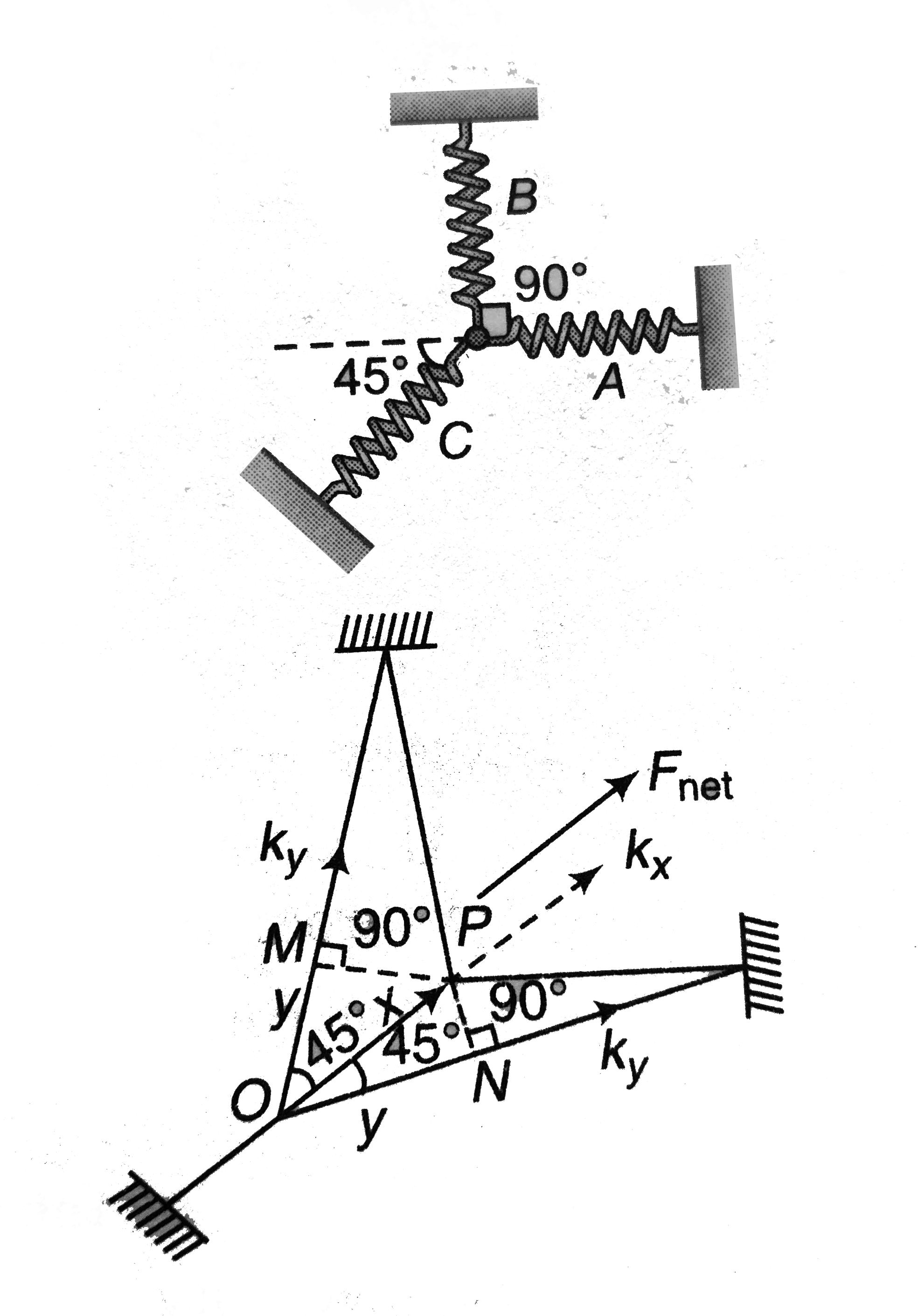 . View Solution
. View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mk - Question 2 - Select One
Three springs of each force constant k are connected as shown figure. Point mass m is slightly displaced to compress A and released. Time period of oscillation is
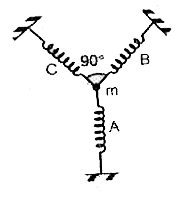 A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1)
A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1) - Question 3 - Select One
A particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mk
A block of mass m is attached to three springs A,B and C having force constants k,k and 2k respectively as shown in figure. If the block is slightly oushed against spring C. If the angular frequency of oscillations is √Nkm, then find N. The system is placed on horizontal smooth surface.
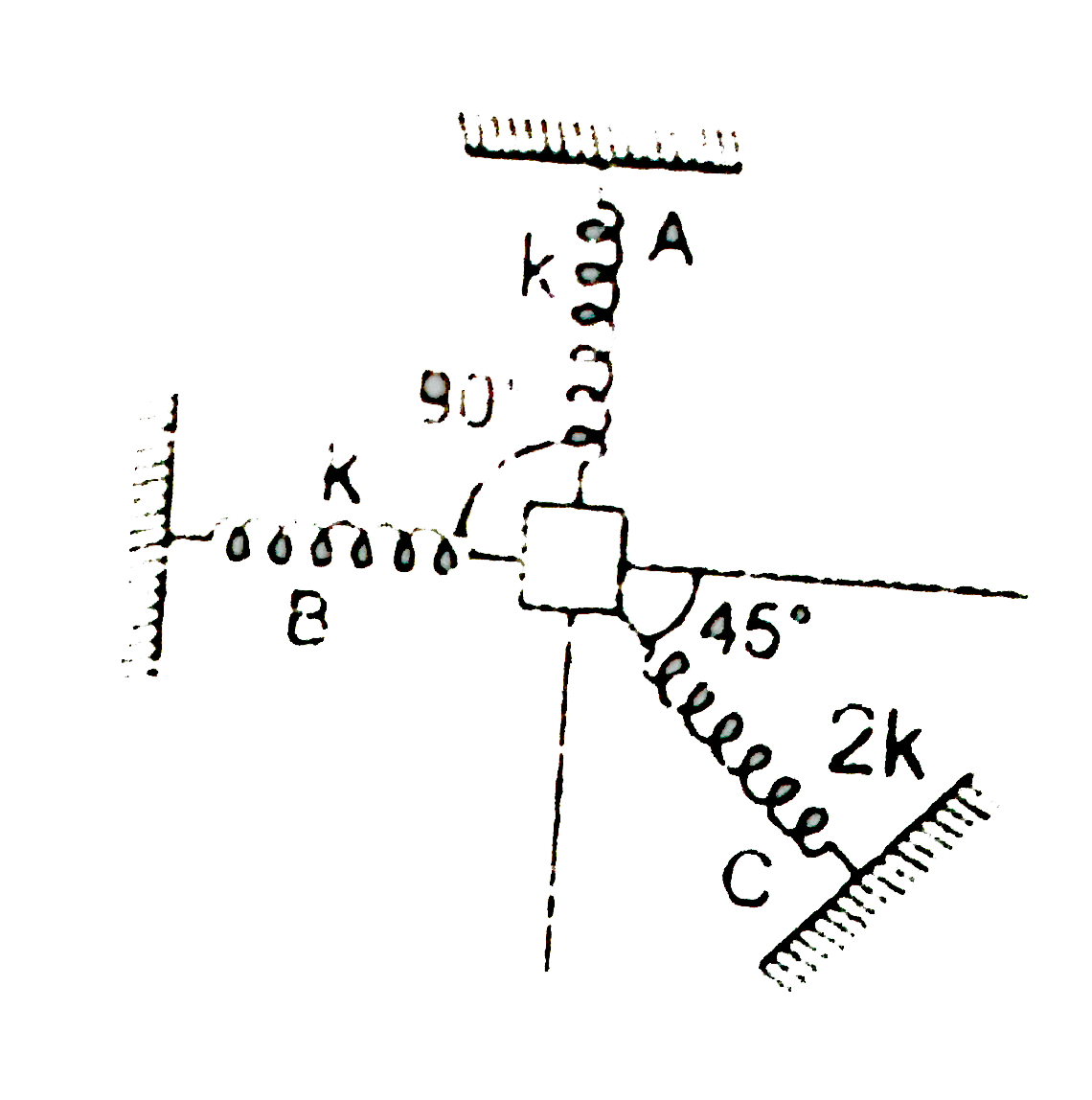 View Solution
View SolutionTwo blocks each of mass m are connected with springs each of force constant K as shown in fig. The mass A is displaced to the left & B to the right by the same amount and released then the time period of oscillation is -
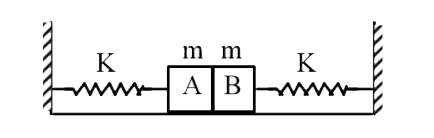 View Solution
View SolutionA body of mass 'm' hangs from three springs, each of spring constant 'k' as shown in the figure. If the mass is slightly displaced and let go, the system will oscillate with time period–
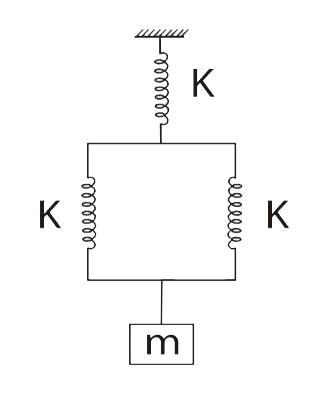 View Solution
View SolutionA block of mass m is suspended by different springs of force constant shown in figure.
 View Solution
View SolutionA body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is
 View Solution
View Solution

