Find the displacement equation of the simple harmonic motion obtained by combining the motions.
x1=2sinωt,x2=4sin (ωt+π6)
and x3=6sin(ωt+π3)
The resultant equation is ,
x=Asin(ωt+ϕ)
∑Ax=2+4cos30∘+6cos60∘=8.46
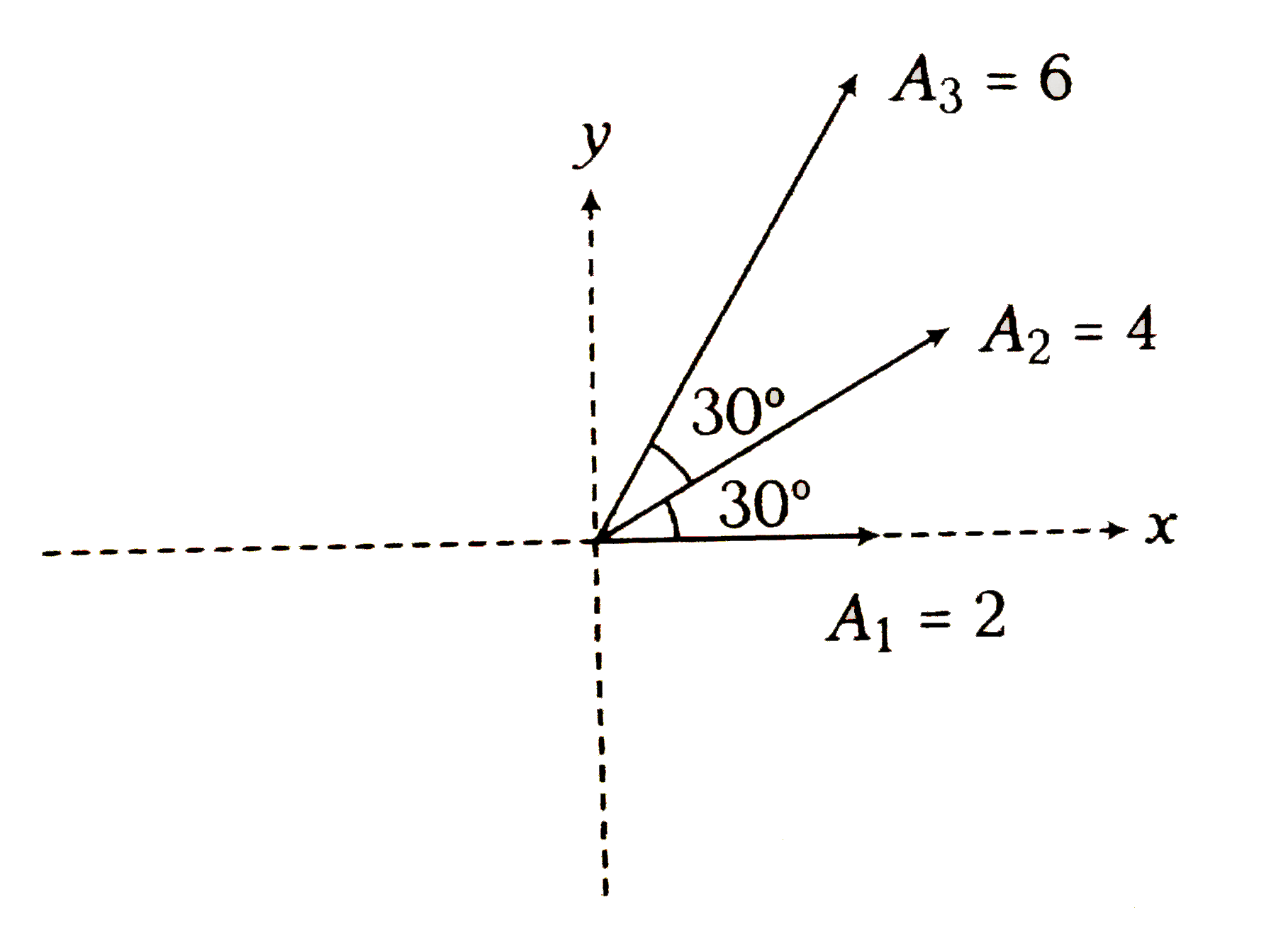
and ∑Ay=4sin30∘+6sin60∘=7.2
∴A=√(∑Ax)2+(∑Ay)2
=√(8.46)2+(7.2)2=11.25
and tanϕ=∑Ay∑Ax=7.28.46=085
or ϕ=tan−1(0.85)=40.4∘
Thus, the displacement equation of the combined motion is,
x=Asin(ωt+ϕ)
x=11.25sin(ωt+ϕ)
where ϕ=40.4∘
Similar Questions
Find the displacement equation of the simple harmonic motion obtained by combining the motions.
x1=2sinωt,x2=4sin (ωt+π6)
and x3=6sin(ωt+π3)
View SolutionFind the displacement equation of the simple harmonic motion obtained by combining the motion.
x1=2sinωt, x2=4sin(ωt+π6) and x3=6sin(ωt+π3)
View Solution
Knowledge Check
Choose the most appropriate option.
What will be the displacement equation, of the simple harmonic motion obtained by combining the motions?
x1=2sinωt,x2=4sin(ωt+π6)
x3=6sin(ωt+π3)Ax=10.25sin(ωt+ϕ)Bx=10.25sin(ωt−ϕ)Cx=11.25sin(ωt+ϕ)Dx=11.25sin(ωt−ϕ)What is the phase difference between two simple harmonic motions represented by x1=Asin(ωt+π6) and x2=Acosωt?
Aπ6Bπ3Cπ2D2π3Find the resultant amplitude of the following simple harmonic equations :
x1=5sinωt
x2=5sin(ωt+53∘)
x3=−10cosωtA5B10C15D20
Find the amplitude of the simple harmonic motion obtasined by combining the motions
x1=(2.0cm)sinωt
andx2=(2.0cm)sin(ωtπ3)
View SolutionFind the amplitude of the harmonic motion obtained by combining the motions
x1=(2.0cm)sinωt
and x2=(2.0cm)sin(ωt+π/3).
View SolutionIf current 11=3A sin ωtand12=4Acosωt,then13 is
View SolutionWhat is the phase difference between two simple harmonic motions represented by x1=Asin(ωt+π6) and x2=Acos(ωt)?
View SolutionThe displacement equation of a simple harmonic oscillator is given by y=Asinωt−Bcosωt
The amplitude of the oscillator will be
View Solution

