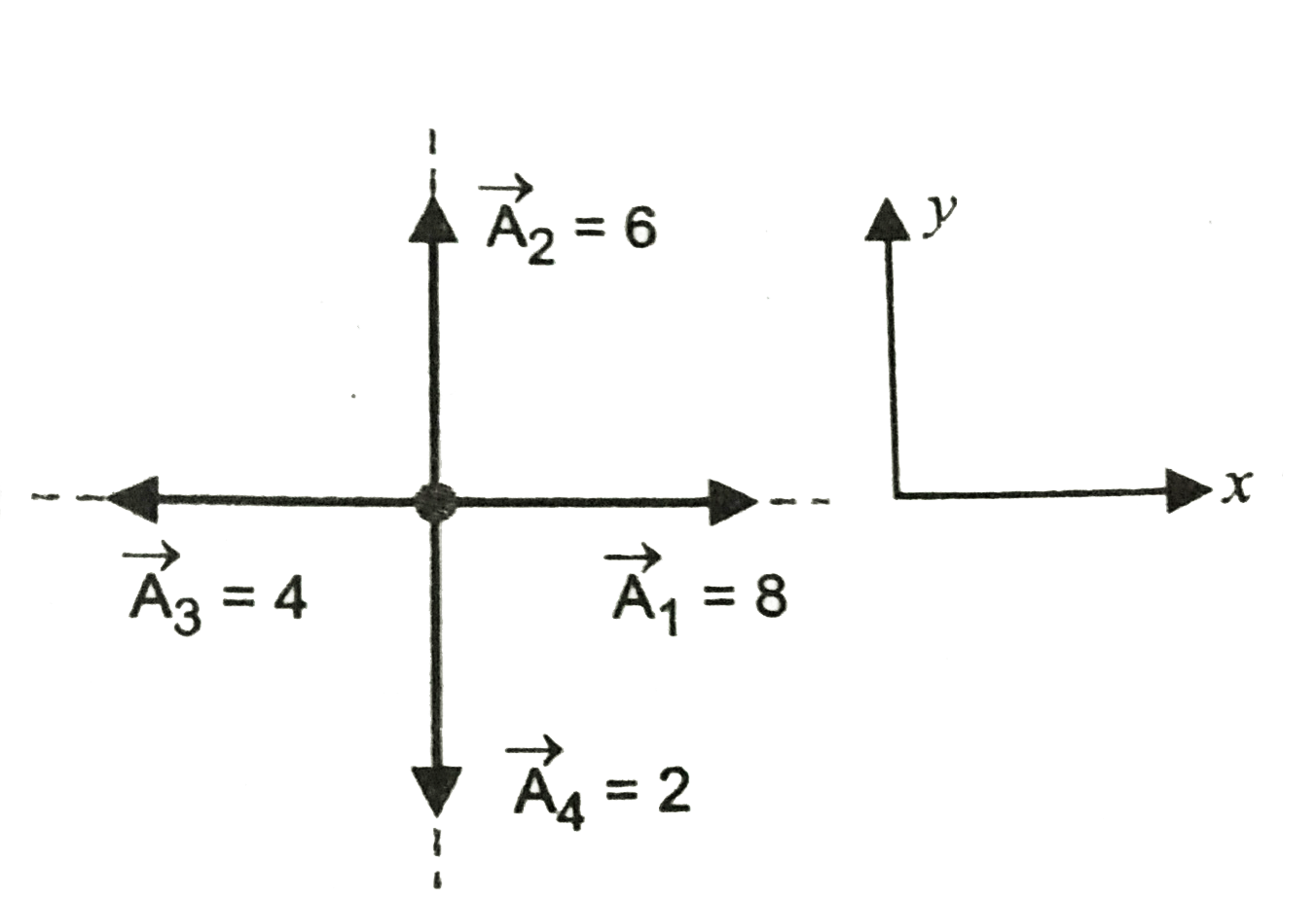
Four simple harmonic motions $, c_{1} = 8 sin ω t, x_{2} = 6 sin (ω t = π / 2), x_{3} = 4 sin (ω t + π) and x_{4} = 2 sin (ω t + 3 π / 2)$ are superimposed on each other. The resuslting amplitude and its phase difference with $x_{1}$ are respectively

$20, {tan}^{- 1} (1 / 2)$

$4 \sqrt{2}, π / 2$

$20, {tan}^{- 1} (2)$

$4 \sqrt{2}, π / 4$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Updated on:21/07/2023

Four simple harmonic vibrations $x_{1} = 8 sin ω t$ , $x_{2} = 6 sin (ω t + \frac{π}{2})$ , $x_{3} = 4 sin (ω t + π)$ and $x_{4} = 2 sin (ω t + \frac{3 π}{2})$ are superimposed on each other. The resulting amplitude and its phase difference with $x_{1}$ are respectively
A $20, {tan}^{- 1} (\frac{1}{2})$
B $4 \sqrt{2}, \frac{π}{2}$
C $20, {tan}^{- 1} (2)$
D $4 \sqrt{2}, \frac{π}{4}$
Four simple harmonic vibrations
$x_{1} = 8 s in (ω t), x_{2} = 6 sin (ω t + \frac{π}{2})$ ,
$x_{3} = 4 sin (ω t + π)$ and $x_{4} = 2 sin (ω t + \frac{3 π}{2})$ are superimposed on each other. The resulting amplitude is……units.
A $20$
B $8 \sqrt{2}$
C $4 \sqrt{2}$
D $4$
For simple harmonic vibrations
$y_{1} = 8 cos ω t$
$y_{2} = 4 cos (ω t + \frac{π}{2})$
$y_{3} = 2 cos (ω t + π)$
$y_{4} = cos (ω t + \frac{3 π}{2})$ are superimposed on one another. The resulting amplitude and phase are respectively
A $\sqrt{45} and {tan}^{- 1} (\frac{1}{2})$
B $\sqrt{45} and {tan}^{- 1} (\frac{1}{3})$
C $\sqrt{75} and {tan}^{- 1} (2)$
D $\sqrt{75} and {tan}^{- 1} (\frac{1}{3})$