A block with a mass of 3.00kg is suspended from an ideal spring having negligible mass and stretches the spring by 0.2m.
(a) What is the force constant of the spring?
(b) What is the period of oscillation of the block if it is pulled down and released ?
(i) In equlibrium , kl=mg∴k=mgl
Substituting the proper values, we have
k=(3)(9.8)0.2=147Nm−1
(ii) T=2π√lg=2π√0.29.8=0.897s
Similar Questions
A mass of 2 kg is suspended from a vertical spring. An additional force of 2.5 N stretches it by 1 cm. (i) Calculate the force constant. (ii) Calculate the frequecny of oscillations, if the spring is stretched by the given force and then released.
View Solution
The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks is
View Solution
Knowledge Check
When a mass of 5 kg is suspended from a spring of negligible mass and spring constant K, it oscillates with a periodic time 2π. If the mass is removed, the length of the spring will decrease by
AgK metreBg metreC2π metreDmK metreA mass M is suspended from a massless spring. An additional mass m stretches the spring further by a distance x. The combined mass will oscillate with a period
A2π ⎷{(M+m)xmg}B2π ⎷{mg(M+m)x}C2π ⎷{(M+m)mgx}Dπ2 ⎷{mg(M+m)x}When a mass of 1 kg is suspended from a spring, it is stretched by 0.4m. A mass of 0.25 kg is suspended from the spring and the spring is allowed to oscillate. If g=10m/s2, then its period of oscillation will be
A0.5 secB0.4 secC0.628 secD1.5 sec
A block of 2 kg is suspended from the ceiling trhough a massless spring of spring constant k=100 N/m. What is the elongation of the spring? If another 1 kg is dded to the block, what would be the further eleongation?
View SolutionA spring mass system has time period of 2 second. What should be the spring constant of spring if the mass of the block is 10grams ?
View SolutionA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View SolutionFind the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
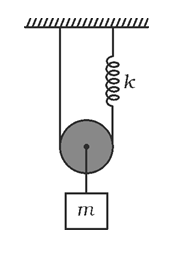
View SolutionA block with mass 0.50kg is forced against a horizontal spring of negligible mass , compressing the spring a distance of 0.20m (figure). When released, the block moves on a horizontal table top for 1.00N/m. What is the coefficient of kinetic friction μk, between the block and the block and the table?

View Solution
