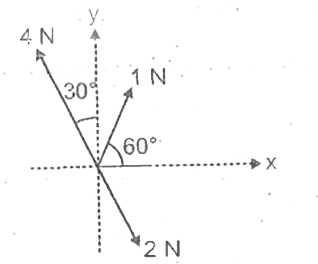
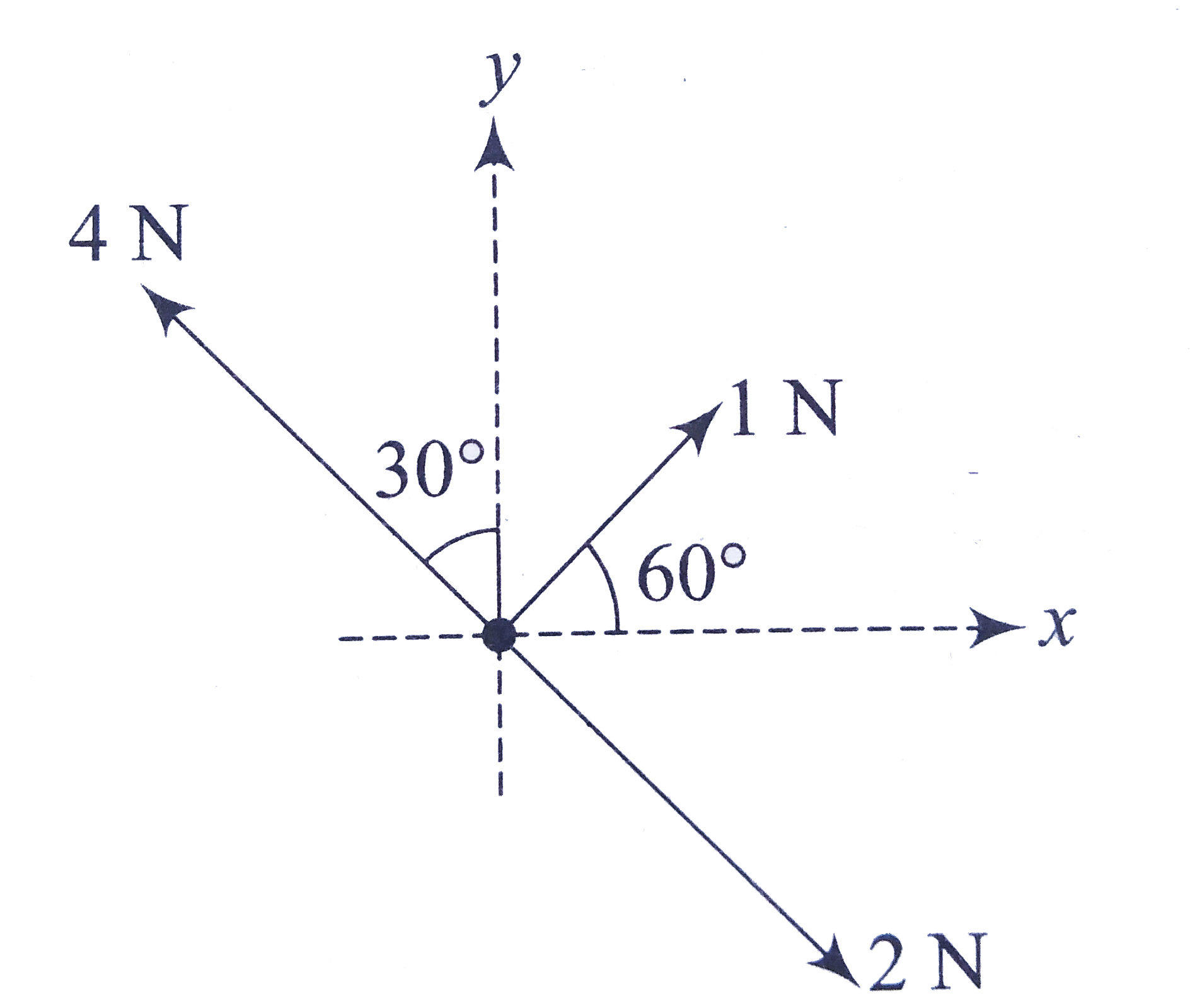
Three forces acting on a body are shown in figure. To have the resultant force only along the y-directon, the magnitude of the minimum additional force needed si
0.5N
1.5N
√34N
√3N
The correct Answer is:A
(a) Minimum additional force needed
F=−(Fresultant)x
Fresultant=[(4−2)(cos30jˆj−sin30ˆi)+(cos60ˆi+sin60ˆj)]
=[2(√32ˆj−12ˆi)+(12ˆi+√32ˆj)]
=[(√3+√32)ˆj+(−ˆi+ˆi2)]
=[−12ˆi+3√32ˆj]=−12+3√32ˆj
⇒Fx=(−ˆi2)
Hence, |F|=0.5N
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.3
20 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.4
20 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.1
20 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
Knowledge Check
Three forces are acting on a particle as shown in the figure. To have the resultant force only along the Y-direction, the magnitude of the maximum additional force needed is
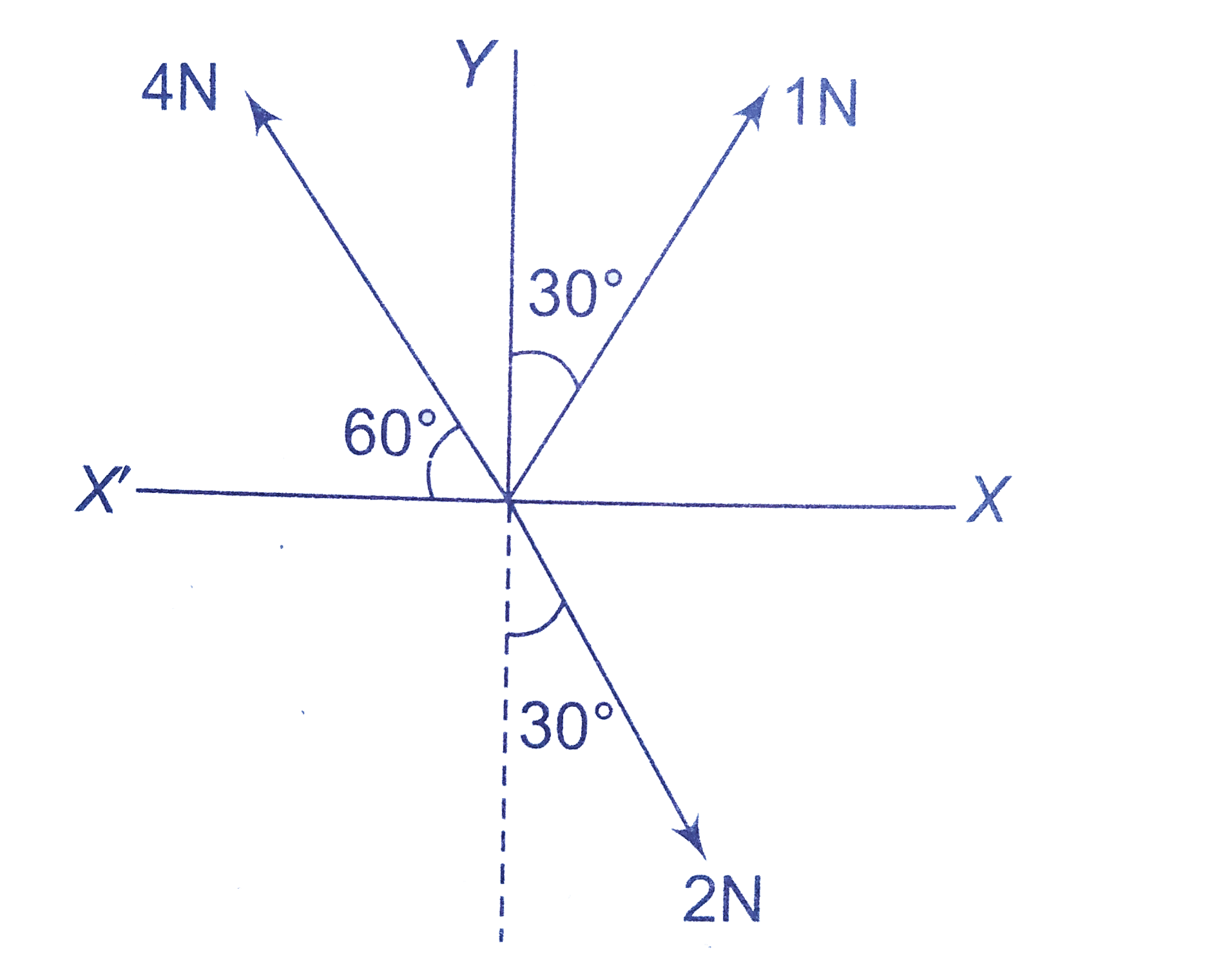 A0.866NB1.732NC0.5ND4N
A0.866NB1.732NC0.5ND4NTwo forces, each equal to F, act as shown in figure. Their resultant is
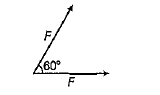 AF/2BFC√3D√5F
AF/2BFC√3D√5FTwo forces, each equal to F, act as shown in (figure) Their resultant is
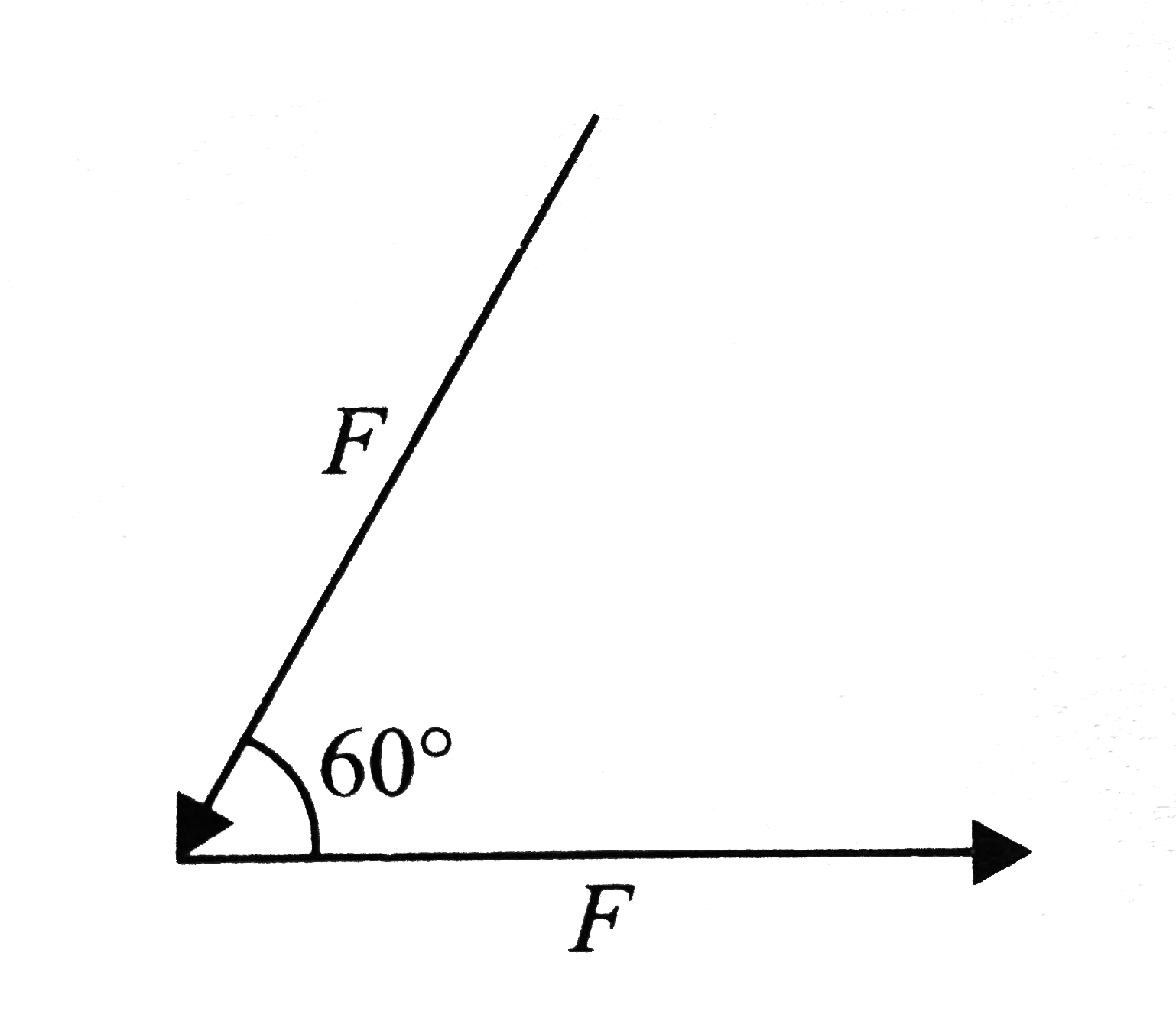 AF/2BFC√3FD√5F
AF/2BFC√3FD√5F
There are four forces acting on a block as shown in the figure ,The magnitude and direction of the net force acting on it is _______.

View SolutionIf two equal forces act on the body in opposite direction, then the resultant force on the body will be
View SolutionAssertion : The forces acting on a body can be replaced by the resultant force only as regards the motion of the body as a whole.
Reason : The resultant force can not replace the several forces acting on a body in other respects.
View SolutionThere are four forces acting on a block as shown in the figure. The magnitude and direction of the net force acting on it is __________.

View SolutionEqual forces F act on isolated bodies A and B as shown in figure. The mass of B is three times that of A. The magnitude of the acceleration of A is:
View Solution