A body is projected upwards with a velocity $u$ . It passes through a certain point above the ground after $t_{1}$ , Find the time after which the body passes through the same point during the journey.

A

$(\frac{u}{g} - t_{1}^{2})$

B

$2 (\frac{u}{g} - t_{1})$

C

$(\frac{u}{g} - t_{1})$

D

$(\frac{u^{2}}{g^{2}} - t_{1})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Velocity of particle of this instant will be $υ = (u - g t_{1})$

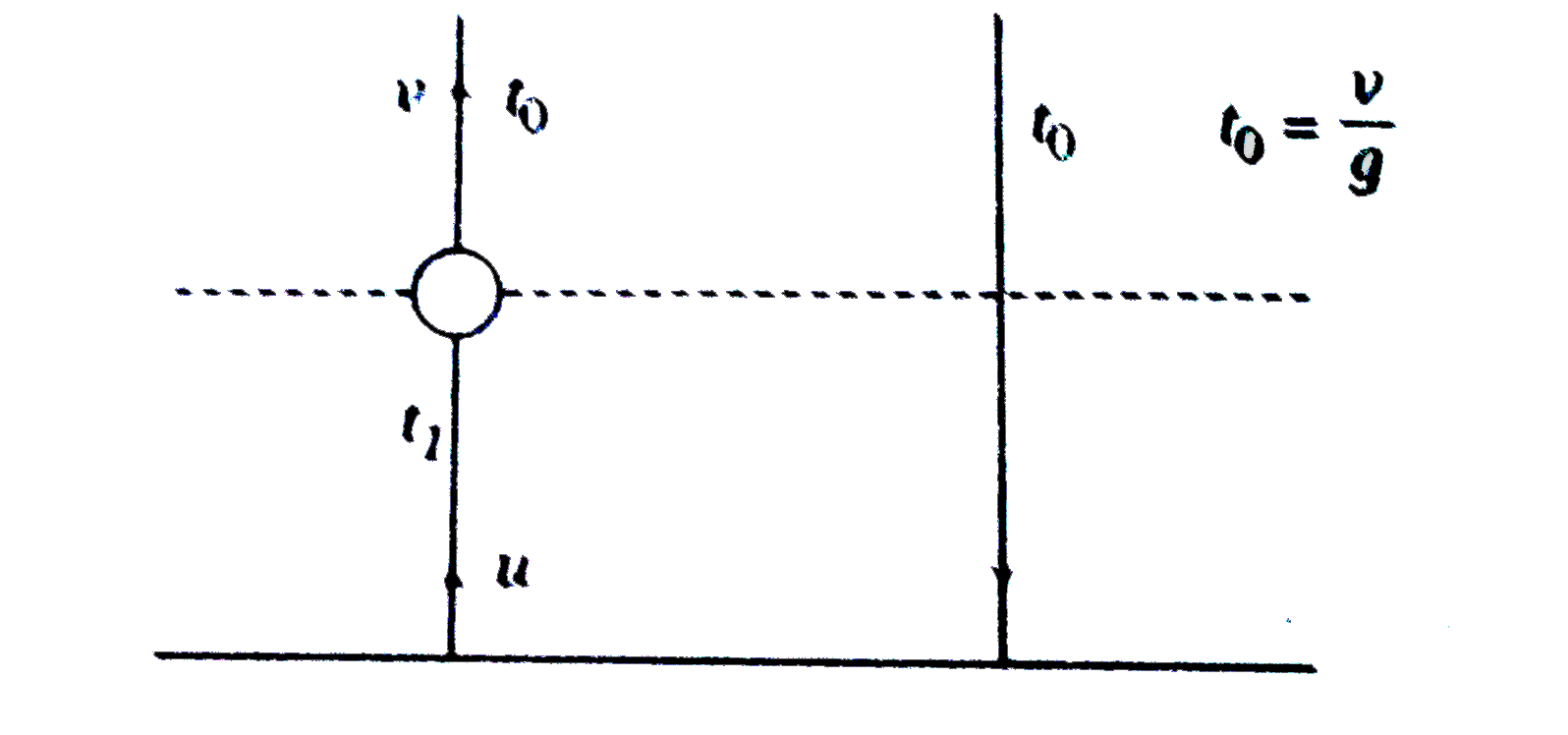
Now the desired time interval will be $\frac{2 υ}{g}$ .
or $\frac{2 (u - g t_{1})}{g} = 2 (\frac{u}{g} - t_{1})$

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A body is projected vertically upwards with some velocity $u$ . It is at the same point at $t = 6 s$ as was at $t = 4 s$ . Find the value of $u$ .
A $30 m / s$
B $40 m / s$
C $20 m / s$
D $50 m / s$
Question 2 - Select One
A body projected vertically upwards with a velocity u returns to the starting point in 4 seconds. If $g = 10 m / sec$ , the value of u is
A $5 m / sec$
B $10 m / sec$
C $15 m / sec$
D $20 m / sec$
Question 3 - Select One
A body is projected vertically upwards with a velocity $u$ it crosses a point in its journey at a height $h$ twice just after 1 and 7 seconds. The value of $u$ in $m s^{- 1}$ is $(g = 10 m s^{- 2})$
A50
B40
C30
D20

DC PANDEY-MOTION IN A PLANE-Check point 3.5

Home
Ask Doubt
Profile