A body is projected up with a speed v0 along the line of greatest slope of an inclined plane of angle of inclination β. If the body collides elastically perpendicular to the inclined plane, find the time after which the body passes through its point of projection.
On striking the plane at B, the velocity along the x - axis should be zero. So using vx=ux+axt, we get
0=mv0cos∝−gsinβT, where T is the time of flight
T=v0cos∝gsinβ…(i)
Also Sy=0 from A to B. So using Sy=uyt+12ayt2, we get
0=(v0sin∝)T−12(gcosβ)T2⇒T=2v0sin∝gcosβ ...(ii)
From (i) and (ii), v0cos∝gcosβ=2v0sin∝gcosβ⇒tan∝=12cotβ
⇒cos∝=2√4+cot2β=2sinβ√2+3sin2β
Put the value of cos∝ in (i) to get T=2v0g√1+3sin2β
Since the body collides elastically, it will rebound perpendicular to the inclined plane with the same speed v. In consequence, it retraces its path elapsing equal time T for backward journey to the point of projection. Hence, the required time of motion is
T'=2T=4v0g√1+3sin2β.
 .
.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Solved Examples
7 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.1
15 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
Find range of projectile on the inclined plane which is projected perpendicular to the incline plane with velcoity 20m/s as shwon in figure.
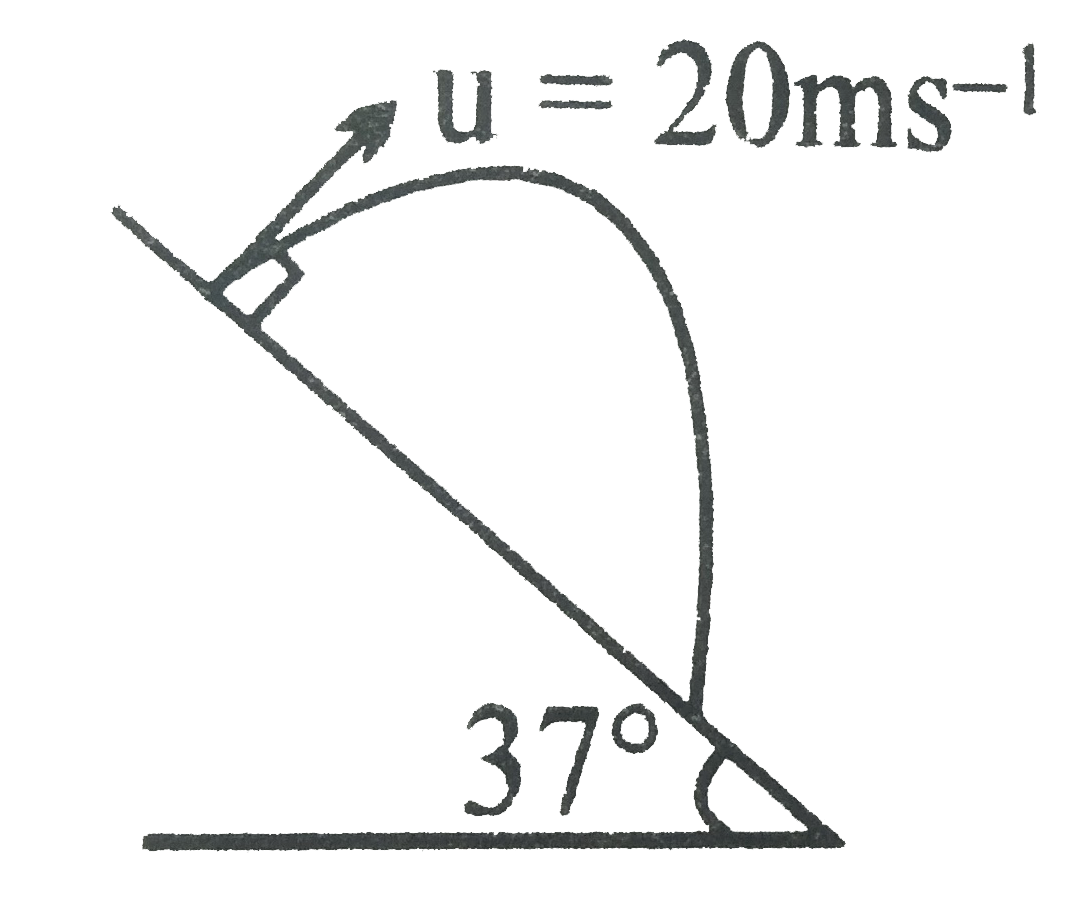
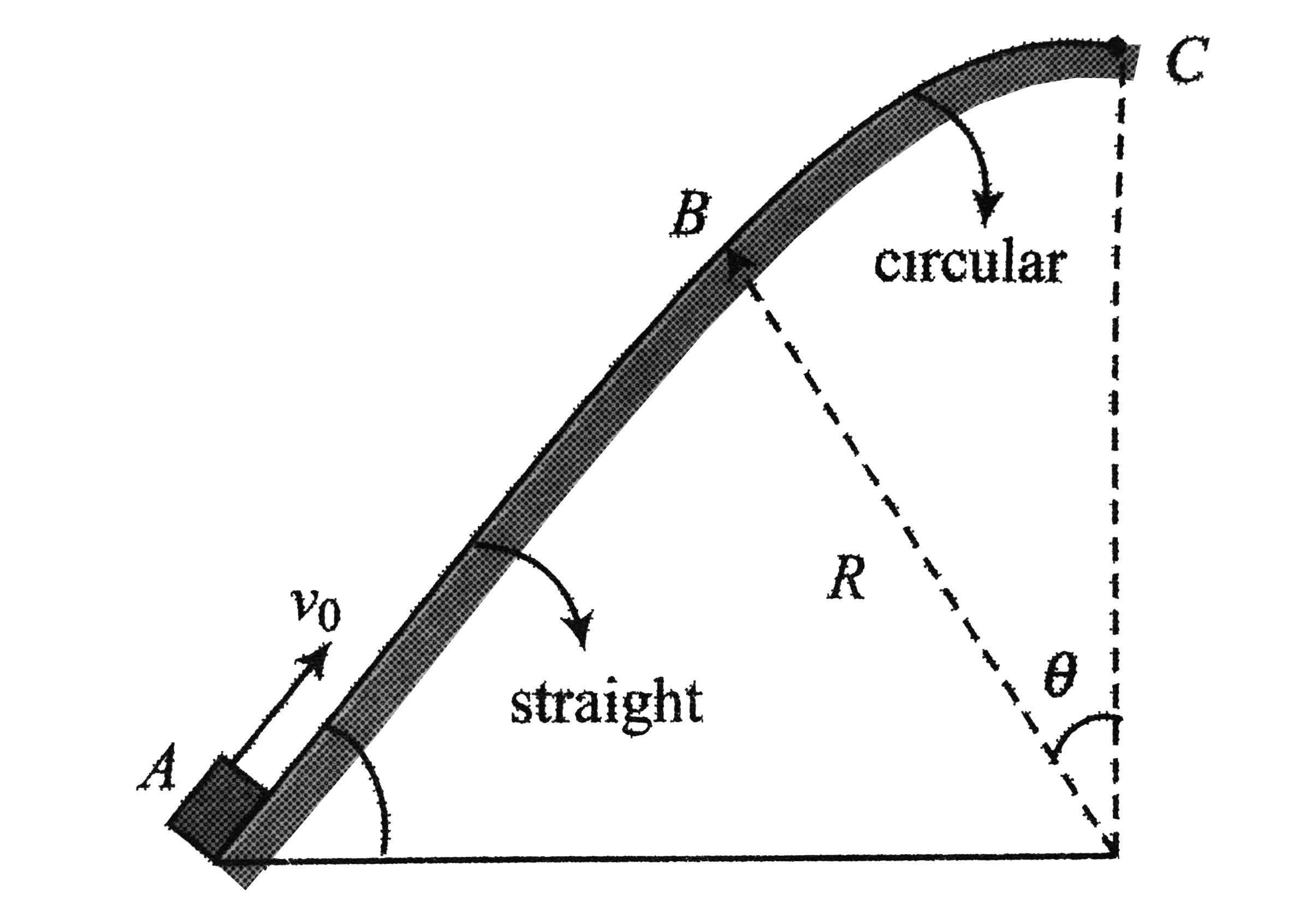
View SolutionA block of mass m is projected up with a velocity v0 along an inclined plane of angle of inclination θ=37∘. The coefficient of friction between the inclined plane AB and blocks is μ(=tanθ). Find the values of v0 so that the block moves in a circular path from B to C.
View Solution
Knowledge Check
A block is projected up along the line of greatest slope of an inclined plane of angle of inclination 0(<ϕ) where ϕ= angle of friction. Which of the following friction time graph is CORRECT ?
A B
B C
C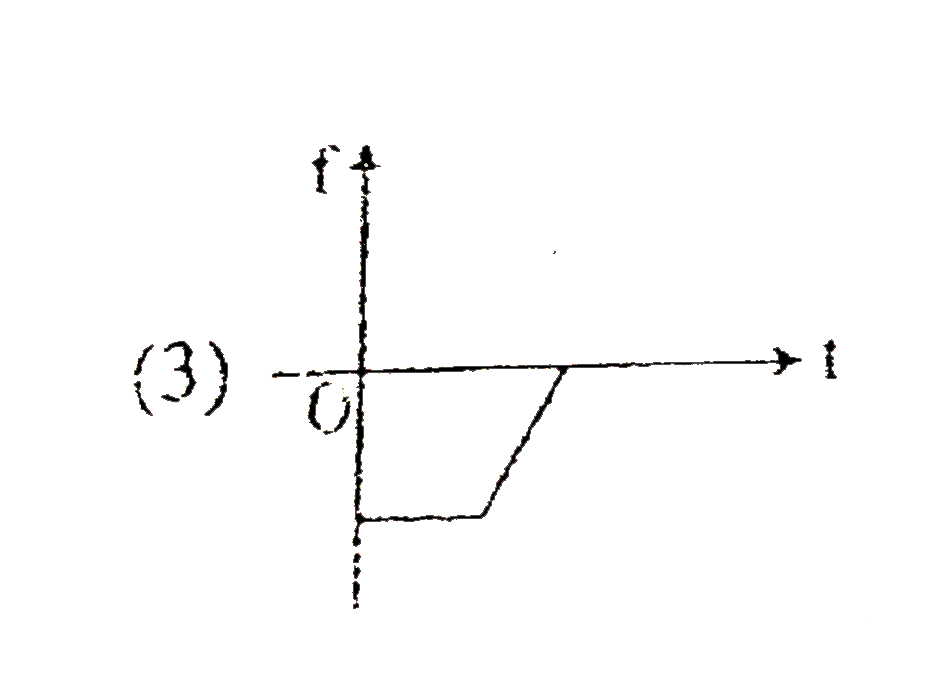 D
D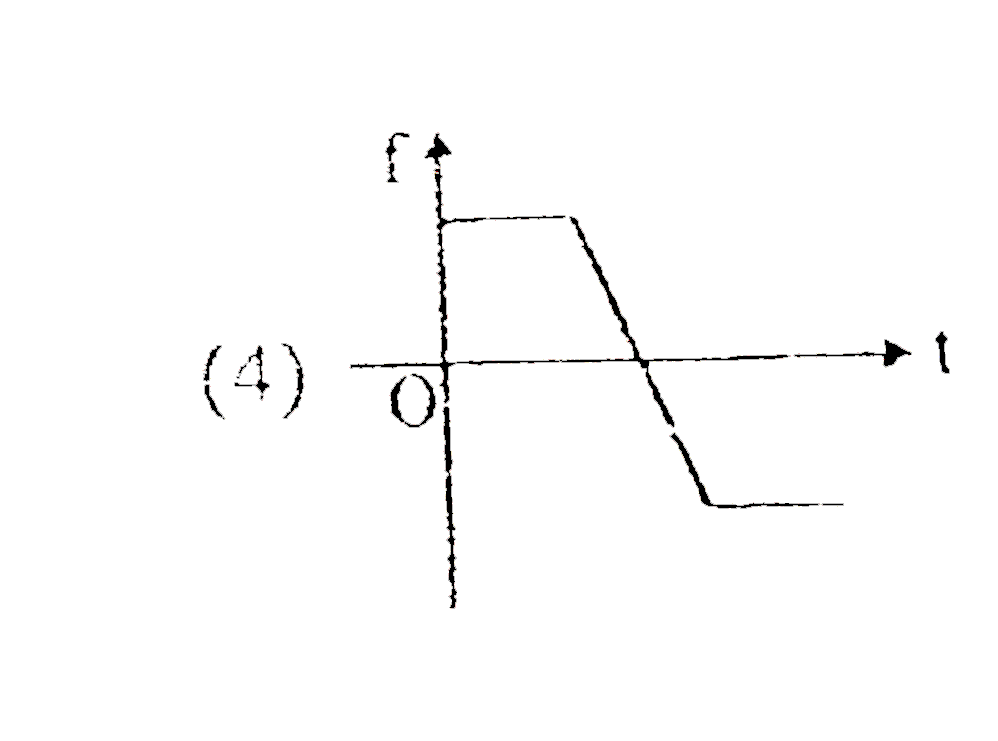
A body of mass 5kg is moved up over 10m along the line of greatest slope of a smooth inclined plane of inclination 30∘ with the horizontal. If g=10m/s2, the work done will be
A500 JB2500 JC250 JD25 JA perfectly elastic particle is projected with a velocity v on a vertical plane through the line of greatest slope of an inclined plane of elevation α.If after striking the plane, the particle rebounds vertically show that it will return to the point of projection at the end of time equal to
A6vg√1+8sin2αB6vg√1+sin2αCvg√1+8sin2αDvg√1+sin2α
A particle is projected along the line of greatest slope up a rough plane inclined at an angle of 45∘ with the horizontal. If the coefficient of friction is 1/2 . Their retardation is:
View SolutionA projectile is projected with speed u at an angle of 60∘ with horizontal from the foot of an inclined plane. If the projectile hits the inclined plane horizontally, the range on inclined plane will be.
View SolutionA particle is projected with a velocity u from the foot of an inclined plane whose inclination to the horizon is β. It strikes. the plane at right angles if
View SolutionA body is freely rolling down on an inclined plane whose angle of inclination is θ. If a is acceleration of its centre of mass then following is correct
View SolutionThe line of greatest slope on an inclined plane P1 is the line in the plane P1 which is perpendicular to the line of intersection of the plane P1 and a horizontal planeP2.
Q. The coordinate of a point on the plane 2x+y−5z=0,2√11 unit away from the line of intersection of 2x+y−5z=0and4x−3y+7z=0 are
View Solution
