A uniform cylinder of radius 1 m, mass 1 kg spins about its axis with an angular velocity 20 rad/s. At certain moment, the cylinder is placed into a corner as shown in the figure. The coefficient of friction between the horizontal wall and the cylinder is $μ$ , whereas the vertical wall is frictionless. If the number of rounds made by the cylinder is 5 before it stops, then the value of $μ$ is (acceleration due to gravity, $g = 10 m / s^{2}$ )
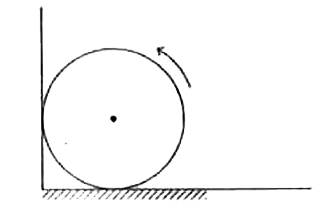Solution in Telugu

A

$\frac{3}{π}$

B

$\frac{2}{π}$

C

$\frac{1}{π}$

D

$\frac{0.4}{π}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Free body diagram of cylinder is

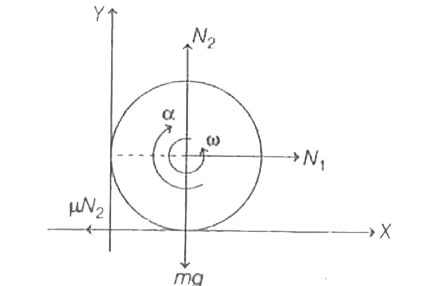
We have following equation
$N_{2} = m g$ …(i)
$μ N_{2} = N_{1} \dots . (i i)$
Torque about centre of cylinder is
$μ N_{2} R = \frac{m R^{2}}{2} α ... . . (i i i i)$
From eqs, (i) and (iii) , we get
$μ m g R = \frac{m R^{2}}{2} α \Rightarrow α = \frac{2 μ g}{R}$
Now using
$ω^{2} = ω_{0}^{2} - 2 α θ$
we have , $0 = {(20)}^{2} - 2 (\frac{2 \times μ \times 10}{1}) θ$
Here , $θ = 5 \times 2 π$
so , ${(20)}^{2} = 40 \times 10 π (μ) \Rightarrow μ = \frac{1}{π}$

Updated on:21/07/2023

|

Class 12 PHYSICS TS EAMCET ENGINEERING ENTRANCE EXAM QUESTION PAPER (2018)

Topper's Solved these Questions

Similar Questions

TS EAMCET PREVIOUS YEAR PAPERS-TS EAMCET ENGINEERING ENTRANCE EXAM QUESTION PAPER (2018)-PHYSICS

Home
Ask Doubt
Profile