A non-conducting solid sphere has radius R and uniform charge density. A spherical cavity of radius R4 is hollowed out of the sphere. The distance between center of cavity is R2. If the charge of the sphere is Q after the creation of the cavity and the magnitude of electric field at the center of the cavity is E=K(Q4π∈0R2), determined the approximate value of K. Solution in Telugu
0.32
0.78
0.51
0.45
The correct Answer is:C
A cavity of radius R4 is made inside a non-conducting solid sphere as shown in the figure.
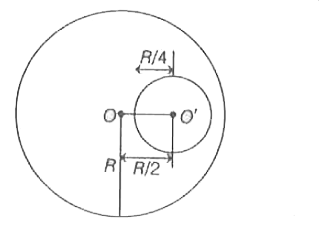
Let Q0 be the charge, present on the sphere when cavity was absent.
Hence, E=EQ0−Ecavity
Where, E= electric field at centre of cavity.
EQ0= electric field at a distance R2 from centre and
Ecavity= electric field due to cavity itself at its centre.
Hence, E=Q04πε0R3(R2)−0
⇒E=Q04πε0R2(12) ...(i)
Now, it is given that Q be the charge after the creation of the cavity.
So, QQ0=43π(R3−(R4)3)43πR3
∴ Since, for a uniform charged density object, charge ∝ volume
⇒QQ0=6364
⇒Q0=Q6463 ...(ii)
So, from the Eq. (i) and (ii) , we get
E=Q4πε0R2(6463×12)
=0.5079[Q4πε0R2)
⇒E=0.51[Q4πε0R2]
Hence, K=0.51
∴ So, the correct option is (c).
Topper's Solved these Questions
Similar Questions
The pressure on a circular plate is measured by measuring the force on the plate and the radius of the plate. If the errors in measurement of the force and the radius are 5% and 3% respectively, the percentage of error in the measurement of pressure is
View SolutionAssertion (A) The number 0.00764 has three significant figures.
Reason (R ) If the number is less than 1, the zeros on the right of the decimal point but to the left of the first non-zero digit are not significant.
View SolutionTwo spherical cavities of radii a and b are hollowed out from the interior of a neutral conducting sphere of radius R. At the center of each cavity , a point charge is placed . Call these charges qa and qb.
The electric field inside the cavity of radius a at a distance r from the center of cavity is

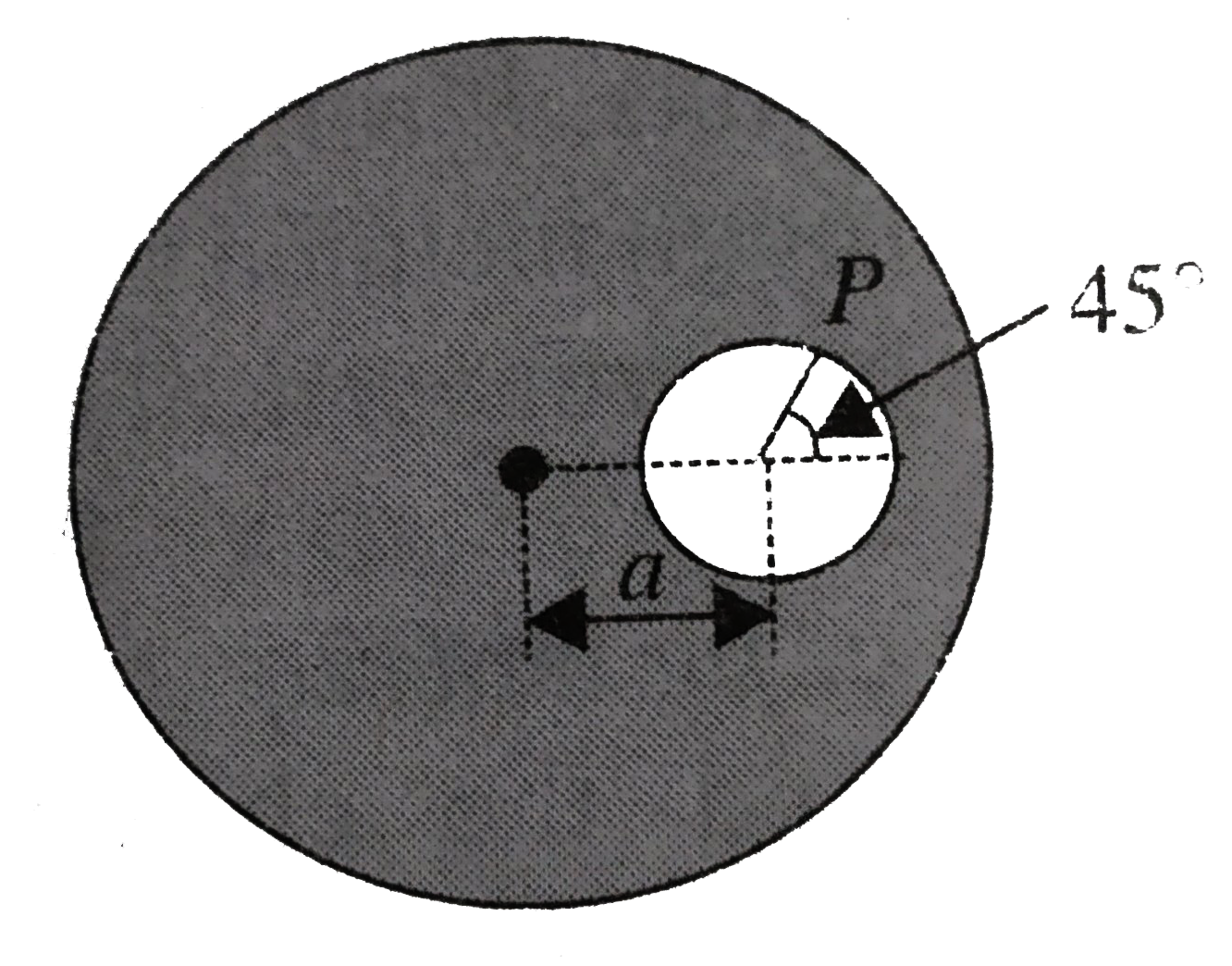
View SolutionA cavity of radius r is made inside a solid sphere. The volume charge density of the remaining sphere is rho . An electron (charge e, mass m) is released inside the cavity from point P as shown in figure. The centre of sphere and center of cavity are separated by a distance a. The time after which the electron again touches the sphere is
View SolutionA solid sphere of radius 'R' has a cavity of radius R2. The solid part has a uniform charge density 'ρ' and cavity has no charge. Find the electric potential at point 'A'. Also find the electric field (only magnitude) at point 'C' inside the cavity
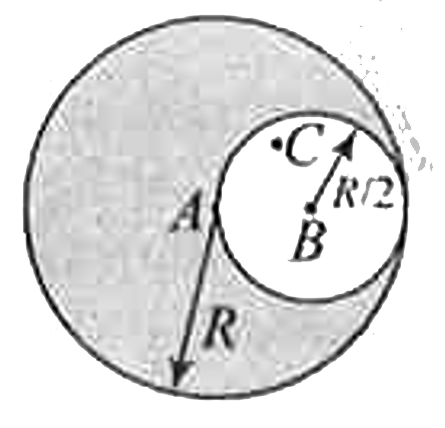
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distanace R/4 from the centre of sphere. The gravitational force on mass m is
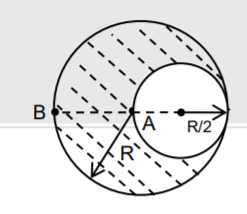
View SolutionA solid sphere having radius R and uniform charge density rho has a cavity of radius R/2 as shown in figure.Find the value of |E_A /E_B|
View SolutionA spherical cavity of radius r is made in a conducting sphere of radius 2 r.A charge q is kept at the centre of cavity as shown in the figure.Find the magnitude of the total electric field at (4r 0) .
View SolutionA conducting sphere of radius R_(2) has a spherical cavity of radius R_(1) which is non concentric with the sphere. A point charge q_(1) is placed at a distance r from the centre of the cavity. For this arrangement, answer the following questions. Electric field (magnitude only) at the center of the cavity will be :
View SolutionA solid sphere having radius R and uniform charge density ρ has a cavity of radius R2 as shown in figure.Find the value of ∣∣∣EAEB∣∣∣
View SolutionIn a positively charged sphere, a positive charge q is located in a spherical cavity. Short distance between the sphere and the center of the cavity vecl is. The charge will be the force on q.
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distanace R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionTwo spherical cavities of radii a and b are hollowed out from the interior of a neutral conducting sphere of radius R. At the center of each cavity , a point charge is placed . Call these charges qa and qb.
The electric field inside the cavity of radius a at a distance r from the center of cavity is

View SolutionA cavity of radius r is made inside a solid sphere. The volume charge density of the remaining sphere is ρ. An electron (charge e, mass m) is released inside the cavity from point P as shown in figure. The centre of sphere and center of cavity are separated by a distance a. The time after which the electron again touches the sphere is
View Solution

