A : loge3+(loge3)22!+(loge3)33!+....=2
R : If x,a∈Randa>0 then ax=1+xlogea+x22!(logea)2+x33!(logea)3+....Solution in Telugu
Both A and R are true and R is the correct explanation of A
Both A and R are true but R is not correct explanation of A
A is true but R is false
A is false but R is true
The correct Answer is:A
Step by step video, text & image solution for A : log_(e)3+((log_(e)3)^(2))/(2!)+((log_(e)3)^(3))/(3!)+....=2 R : If x,ainRandagt0" then "a^(x)=1+xlog_(e)a+(x^(2))/(2!)(log_(e)a)^(2)+(x^(3))/(3!)(log_(e)a)^(3)+.... by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- EXPONENTIAL SERIES & LOGARITHMIC SERIES (APPENDIX-1)BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - EXPONENTIAL SERIES & LOGARITHMIC SERIES (APPENDIX-1)EXERCISE - EXERCISE 2 SET - 3
5 Videos
- ELLIPSEBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - ELLIPSEEXERCISE - EXERCISE 2 SET - 2
1 Videos
- FUNCTIONSBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - FUNCTIONSEXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS)
7 Videos
Similar Questions
Match the following
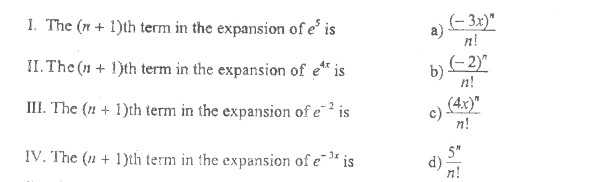
View SolutionThe equation of the chord of contact of the point (1, -2) w.r.t the ellipse 4x2+5y2=20 is
View SolutionI : Ever function must be either even or odd function
The function f(x)=log(x+√x2+1) is an odd function.
View SolutionThe value of e^(log_(e)x+log_(sqrt(2))x)+log_(e^((1)/(3)))x+...+log_(e^((1)/(10)))x)=
View Solution1log3e+1log3e2+1log3e4+...=
View SolutionThe value of
1+(logex)+(logex)22!+(logex)33!+…∞
View SolutionIf a>0andx∈R, then
1+(xlogea)+x22!(logea)2+x33!(logea)3+….∞ is equal to
View SolutionLet x and a be positive real numbers
Statement 1: The sum of theries
1+(logex)22!+(logex)33!+(logex)2+…→∞isx
Statement2: The sum of the series
1+(xlogea)+x22!(logex))2+x33!(logea)33!+→∞isax
View SolutionThe value of 1−loge2+(loge2)22!−(loge2)33!+.. is
View Solutionlog_(e)2+((log_(e)2)^2)/(2!)+((log_(e)2)^(3))/(3!)+....=
View Solutionloge3+(loge3)22!+(loge3)33!+....=
View Solution1+2(logea)+222!(logea)2+233!(logea)3+....=
View Solution1+x(loge2)+x22!(loge2)2+x33!(loge2)3+....=
View Solutionxlogea+x33!(logea)3+x55!(logea)5+...=
View Solution1+xlogea+x22!(logea)2+x33!(logea)3+……बराबर होगा।
View Solution
