In ΔABC,ifrr1=r2r3, then the triangle is Solution in Telugu
only I is true
only II is true
both I, II are true
neither I nor II is true
The correct Answer is:D
Step by step video, text & image solution for In Delta ABC, if r r_1=r_2 r_3, then the triangle is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES OF TRIANGLES Book:DIPTI PUBLICATION ( AP EAMET)Chapter:PROPERTIES OF TRIANGLES Exercise:EXERCISE 2 (SPECIAL TYPE QUESTIONS) Set -2
Explore 5 Videos
- PROPERTIES OF TRIANGLES Book:DIPTI PUBLICATION ( AP EAMET)Chapter:PROPERTIES OF TRIANGLES Exercise:EXERCISE 2 (SPECIAL TYPE QUESTIONS) Set -3
Explore 7 Videos
- PROPERTIES OF TRIANGLES Book:DIPTI PUBLICATION ( AP EAMET)Chapter:PROPERTIES OF TRIANGLES Exercise:EXERCISE 1C
Explore 45 Videos
- PRODUCTS OF VECTORSBook:DIPTI PUBLICATION ( AP EAMET)Chapter:PRODUCTS OF VECTORSExercise:Exercise 2 (Special Type Questions) SET -D
Explore 14 Videos
- QUADRATIC EXPRESSIONSBook:DIPTI PUBLICATION ( AP EAMET)Chapter:QUADRATIC EXPRESSIONSExercise:EXERCISE 2 ( SPECIAL TYPE QUESTIONOS ) ( SET -4)
Explore 4 Videos
Similar Questions
The ascending order of α=cotA2cotC2 when s=4b,β=cotB2cotC2 when s=3a, γ=cosA−C2cosecB2 When a,b,c are in A.P.is
View SolutionMatch the following
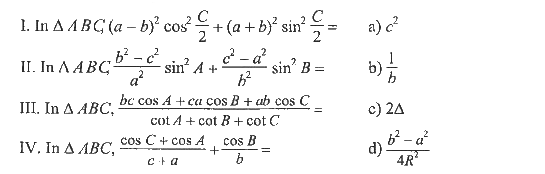
View SolutionFrom the top a mast of 180 mt high, the angle of depression of an object is 60∘ The distance of the object from the ship is
View SolutionA : Angle between the vectors I - 2j + k, 2i - j - k is π3.
R : If θ is the angle between a,b then cos θ=a.b|a||b|
View SolutionA: The quadratic equation having roots 3±2I is x2−6x+13=0
R : the quadratic equation having roots α,β is x2−(α+β)x+αβ=0
View SolutionIn ΔABC,r(r1+r2+r3)=
View SolutionIn ΔABC,(r1−r)(r2−r)(r3−r)=
View SolutionIn Delta ABC, (r_1+r_2)(r_2+r_3)(r_3+r_1)=
View SolutionIn ΔABC,r+r2+r3−r1=
View SolutionIn ΔABC,r+r2+r3−r1=
View SolutionIn ΔABC,r+r2+r3−r1=
View SolutionIn ΔABC,ab−r1r2r3=
View SolutionIn ΔABC,r1r+r2r3bc=
View SolutionIn ΔABC,r3+r1r2r1+r2=
View SolutionIn ΔABC,ifr1,r2,r3 are in H.P., then r2/r=
View SolutionIn ΔABC,ifr1=r2=r3 then the triangle is
View Solution

