A: The quadratic equation having roots 3±2I is x2−6x+13=0
R : the quadratic equation having roots α,β is x2−(α+β)x+αβ=0Solution in Telugu
Both A are R are ture R is the correct explanation Of A
Both A are R are true but R is not correct explanation of A
A is true but R is false
A is false but R is true
The correct Answer is:A
Step by step video, text & image solution for A: The quadratic equation having roots 3 +-2 I is x^2 -6x +13 =0 R : the quadratic equation having roots alpha , beta is x^2 -( alpha + beta ) x + alpha beta =0 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRATIC EXPRESSIONSBook:DIPTI PUBLICATION ( AP EAMET)Chapter:QUADRATIC EXPRESSIONSExercise:EXERCISE 2 ( SPECIAL TYPE QUESTIONOS ) ( SET -3)
Explore 4 Videos
- PROPERTIES OF TRIANGLES Book:DIPTI PUBLICATION ( AP EAMET)Chapter:PROPERTIES OF TRIANGLES Exercise:EXERCISE 2 (SPECIAL TYPE QUESTIONS) Set-4
Explore 10 Videos
- RELATIONSBook:DIPTI PUBLICATION ( AP EAMET)Chapter:RELATIONSExercise:Exercise
Explore 49 Videos
Similar Questions
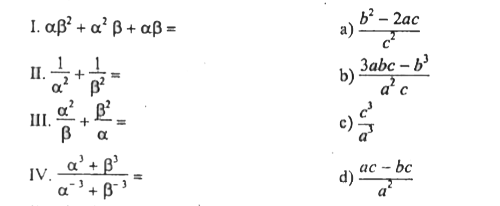
IF α,β are the roots of ax2+bx+c=0 then the match the following
View SolutionA: In a ΔABC, if the sides a,b,c are in A.P. then acos2C2+ccos2A2=3b
R: In a ΔABC, if A,B,C are in A.P. then B=π/3
View SolutionIf A ={1,2,3},B={x,y} then A×B=
View SolutionIf alpha and beta are the roots of equation x^(2)-4x+13=0, then quadratic equation x^(2)-4x+13=0, then quadratic equation whose root ate alpha^(4)-4 alpha^(3)+13 alpha^(2)+2 and (beta^(3)-4 beta^(2)+13 beta+1)/(4) is
View SolutionIf alpha and beta are the roots of the quadratic equation x^(2)-6x+1=0, then the value of (alpha^(2))/(beta^(2))+(beta^(2))/(alpha^(2)) is
View SolutionIf alpha and beta are the roots of the quadratic equation x^(2)-3x-2=0, then (alpha)/(beta)+(beta)/(alpha)=
View Solutionif alpha and beta are the roots of the quadratic equation x^(2)-3.x-2=0, find a quadratic equation whose roots are (1)/(2 alpha+beta) and (1)/(2 beta+alpha)
View SolutionIf α and β are the roots of the quadratic equation x2−5x+6=0 then find αβ+βα
View SolutionIf αandβ are roots of the quadratic equation x2+4x+3=0, then the equation whose roots are 2α+βandα+2β is :
View SolutionThe roots of the equation x2+6x−4=0 are α,β. Find the quadratic equation whose roots area
α2andβ2
View SolutionIf α,β are the roots of x2−x+1=0 then the quadratic equation whose roots are α2015,β2015 is
View SolutionIf α,β are the roots of x2−x+1=0 then the quadratic equation whose roots are α2015,β2015 is
View SolutionIf α,β are the roots of x2−x+1=0, then the quadratic equation whose roots are α2015β2015 is
View SolutionIf αandβ are the roots of the quadratic equation x2+√2x+3=0 form a quadratic equation with roots1αand1β
View SolutionIf αandβ are the roots of the equation x2−3x+2=0, Find the quadratic equation whose roots are −αand−β:
View Solution

