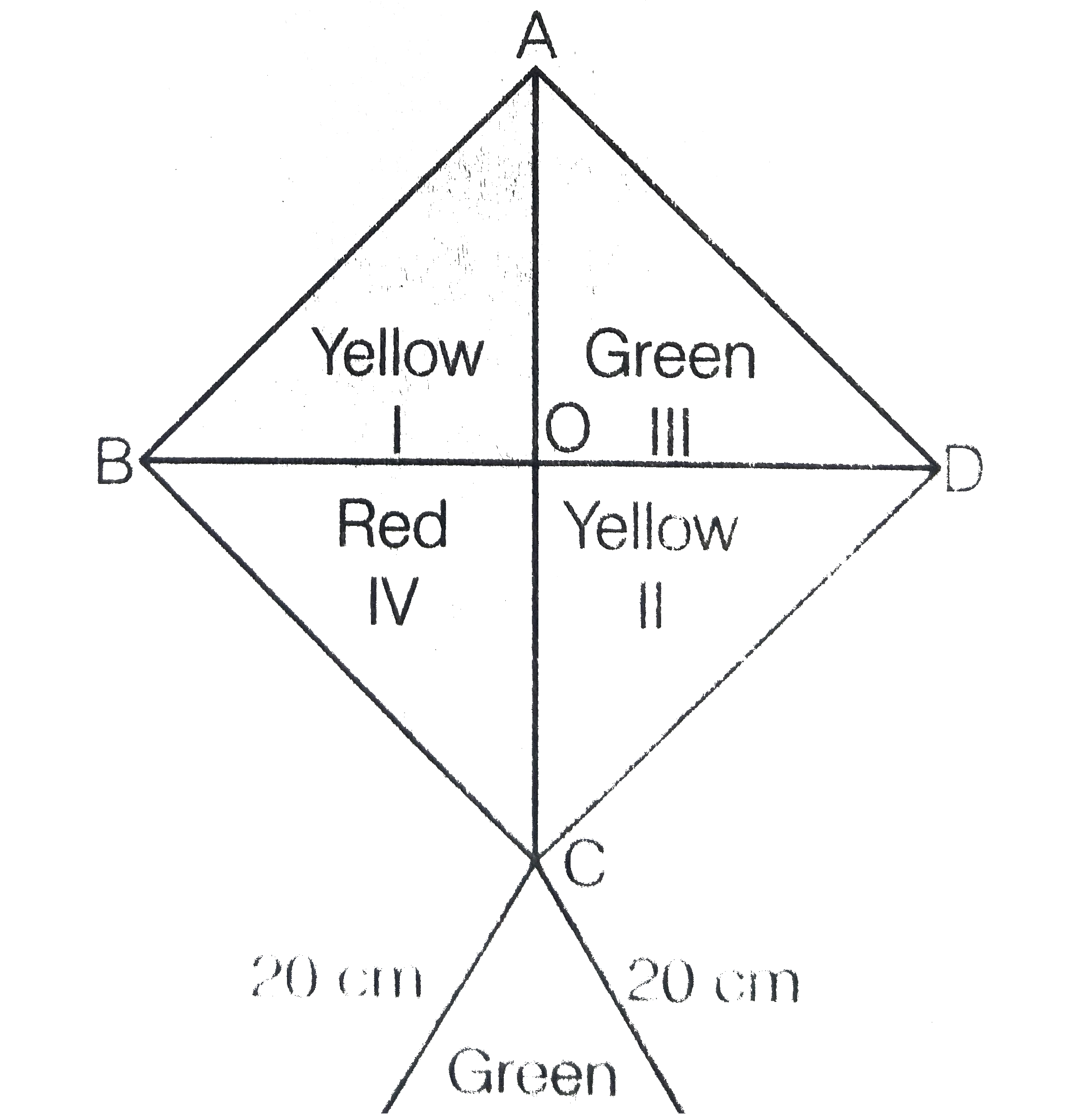
How much paper of each shade is needed to make a kite given in the figure, in which ABCD is a square with diagonal 44cm2
To find out how much paper of each shade is needed to make the kite, we need to calculate the areas of the different regions (yellow, green, red) based on the given square ABCD with a diagonal of 44 cm.
1. Calculate the Area of Square ABCD:
- The area of a square can be calculated using the formula:
Area=12×d2
where d is the length of the diagonal.
- Given d=44cm:
Area=12×(44)2=12×1936=968cm2
2. Calculate the Area of the Red Region:
- The red region is one-fourth of the area of the square ABCD:
Area of Red=14×968=242cm2
3. Calculate the Area of the Yellow Region:
- The yellow region consists of two parts (Yellow 1 and Yellow 2), each having the same area as the red region:
Area of Yellow=2×Area of Red=2×242=484cm2
4. Calculate the Area of the Green Region:
- The green region consists of a triangle. To find its area, we can use Heron's formula.
- First, we need to find the semi-perimeter s of the triangle formed by the vertices of the square:
- The sides of the triangle are 20cm, 20cm, and 22cm.
s=20+20+222=31cm
- Now, applying Heron's formula:
Area=√s(s−a)(s−b)(s−c)
where a=20, b=20, and c=22:
Area=√31(31−20)(31−20)(31−22)=√31×11×11×9
=√31×121×9=√31×1089≈131.15cm2
5. Total Area of the Green Region:
- The area of the green region is the area of the triangle:
Area of Green=242+131.15=373.15cm2
Summary of Areas:
- Area of Red: 242cm2
- Area of Yellow: 484cm2
- Area of Green: 373.15cm2
- The area of a square can be calculated using the formula:
Area=12×d2
where d is the length of the diagonal.
- Given d=44cm:
Area=12×(44)2=12×1936=968cm2
- The red region is one-fourth of the area of the square ABCD:
Area of Red=14×968=242cm2
- The yellow region consists of two parts (Yellow 1 and Yellow 2), each having the same area as the red region:
Area of Yellow=2×Area of Red=2×242=484cm2
- The green region consists of a triangle. To find its area, we can use Heron's formula.
- First, we need to find the semi-perimeter s of the triangle formed by the vertices of the square:
- The sides of the triangle are 20cm, 20cm, and 22cm.
s=20+20+222=31cm
- Now, applying Heron's formula:
Area=√s(s−a)(s−b)(s−c)
where a=20, b=20, and c=22:
Area=√31(31−20)(31−20)(31−22)=√31×11×11×9
=√31×121×9=√31×1089≈131.15cm2
- The area of the green region is the area of the triangle:
Area of Green=242+131.15=373.15cm2
- Area of Red: 242cm2
- Area of Yellow: 484cm2
- Area of Green: 373.15cm2
Topper's Solved these Questions
- HERONS'S FORMULABOOK - NAGEEN PRAKASHANCHAPTER - HERONS'S FORMULAEXERCISE - Exercise 12a
11 Videos
- HERONS'S FORMULABOOK - NAGEEN PRAKASHANCHAPTER - HERONS'S FORMULAEXERCISE - Exercise 12b
10 Videos
- HERONS'S FORMULABOOK - NAGEEN PRAKASHANCHAPTER - HERONS'S FORMULAEXERCISE - Revision Exercise
11 Videos
- CONSTRUCTIONSBOOK - NAGEEN PRAKASHANCHAPTER - CONSTRUCTIONSEXERCISE - EXAMPLE SOLUTION.
19 Videos
- INTRODUCTION TO EUCLID'S GEOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION TO EUCLID'S GEOMETRYEXERCISE - Exercise
3 Videos
Similar Questions
Knowledge Check
How much part of the given square shaped figure is shaded?
 A12B23C35D49
A12B23C35D49Find the area of the shaded region in fig., where ABCD is a square of side 14 cm and four circles are of same radii each.
A128cm2B192cm2C148cm2D168cm2
Find the area of the shaded region in figure where ABCD is a square of side 14 cm.

View SolutionHow many minimum squares must be shaded to make the given figure symmetric?

View SolutionFind the area of the shaded region as shown in figure, where ABCD is square of side 14 cm.
View SolutionFind the area of the shaded region in the given figure of square ABCD :

View SolutionFind the perimeter of the shaded region in the figure,if ABCD is a square of side 14 cm and APB and CPD are semicircles.

View SolutionConstruct a square in which each diagonal is 5cm long.
View Solution