find of the An archery target has three regions formed by three concentric circles as shown in Fig 15.8. If the diameters of the concentric circles are in the ratio 1:2:3. , then find the ratio of the areas of three regions Fig. 15.8
Let the diameters of concentric circles be k, 2k and 3k.
∴ Radius of concentric circles arek2,kand3k2
∴ Area of innir circle, A1=π(k2)2=k2π4
∴ Area of middle region, A2=π(k)2−k2π4=3k2π4
[∵ area of ring = π(R2−r2) , where R is radius of outer ring and r is radius of inner ring]
and area of outer region, A3=π(3k2)2−πk2
= 9πk24−πk2=5πk24
∴ Required ratio = A1:A2:A3
= k2π4:3k2π4:5πk24=1:3:5
Topper's Solved these Questions
Similar Questions
An archery target has three regions formed by three concentric circles in Fig. 12.73. If the diameters of the concentric circles are in the ratio 1:3:5. then find the ratio of the areas of three regions.

View SolutionIf the diameters of the concentric circles shown in the figure below are in the ratio 1:2:3 then find the ratio of the areas of three regions.

View SolutionThe circumferences of two circles are in the ratio 2:3. Find the ratio of their areas.
View SolutionThe circumference of two circles are in the ratio 2 :3 . Find the ratio of their areas.
View SolutionFind the area of the shaded region shown in the fig.
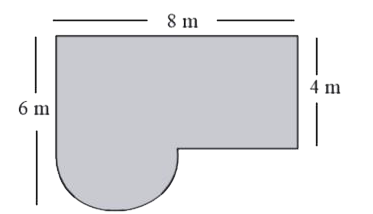
View SolutionThe radii of three concentric circles are in the ratio 1:2:3. Find the ratio of the area between the two inner circles to that between the two outer circles.
View SolutionIn the give figure, the sectors of two concentric circles of radii 7 cm and 3.5 cm are shown. Find the area of the shaded region.

View SolutionThe diameters of two circles are 3.5cm and 6cm .Find the ratio of the area of the larger circle smaller circle.
View SolutionFind the areas of the shaded region in the Fig. 15.39. (FIGURE)
View SolutionFind the relation in the accelerations of the three masses shown in fig.
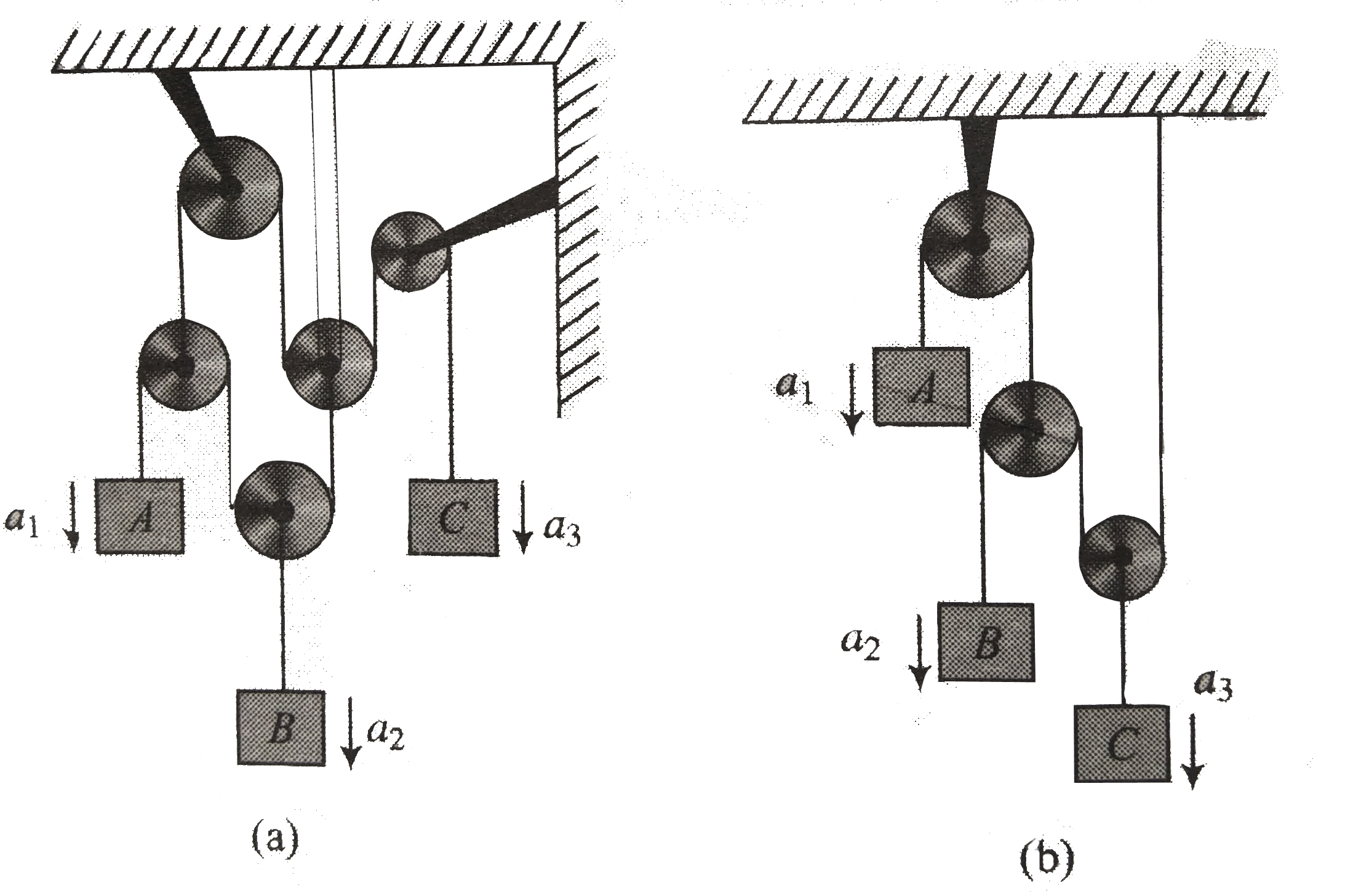
View Solution
