Refer figure. Core has refractive index μ1=1.424. The cladding refractive index μ2=1.39. In such a case. Will the light beam propagate?

Yes
No
Data given insufficient to decide
the beam propagation is not affected with refractive indices of fibre core and cladding.
The correct Answer is:A
If μ1 is the refractiv e index of c ore of optical fibre, then
μ1=sin10osin7o=0.17360.1219=1.424
Critical angle at core and cladding surface in
sinC=μ2μ1=1.391.424=0.9761=sin77∘27'
C=77∘7'
The angle of incidence on core-cladding surface =90∘−7∘=83∘, which is greater than critical single, hence beam will propagation through optical fibre.
Topper's Solved these Questions
- COMMUNITCATION SYSTEMSBOOK - NCERT FINGERTIPSCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - NCERT Exemplar
18 Videos
- COMMUNITCATION SYSTEMSBOOK - NCERT FINGERTIPSCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - Assertion And Reason
30 Videos
- COMMUNITCATION SYSTEMSBOOK - NCERT FINGERTIPSCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - Amplitude Modulation
20 Videos
- ATOMS BOOK - NCERT FINGERTIPSCHAPTER - ATOMS EXERCISE - Assertion And Reason
15 Videos
- CURRENT ELECTRICITYBOOK - NCERT FINGERTIPSCHAPTER - CURRENT ELECTRICITYEXERCISE - Assertion And Reason
15 Videos
Similar Questions
Determine the value of the angle of incident for a ray of light travelling from a medium of refractive index μ1=√2 into the medium of refractive index μ2=1, so that it just grazed along the surface of separation.
View SolutionA thin bi-convex lens made out of a material of refractive index μ1 is place in a medium of refractive index μ2. A paraxial beam of light, parallel to the principal axis of the lens, is shown in the figure. Based on the ray diagram, we can conclude that
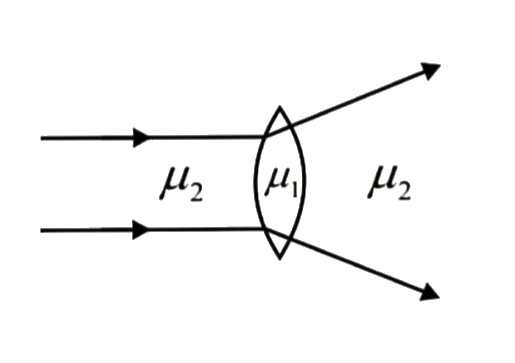
View Solution
Knowledge Check
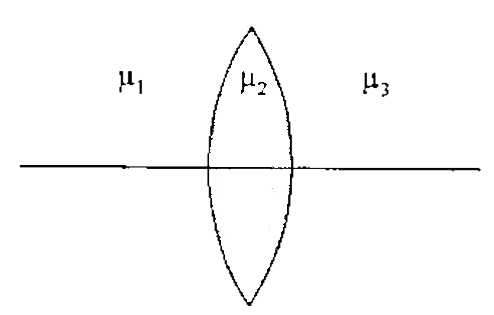
A thin symmettrical double convex lens of refractive index μ2−1.5 is placed between a medium of refractiv eindex μ1=1.4 to the left and another medium of refractive index μ3=1.6 to the right.Then the system behaves as
Aa convex lensBa concave lensCa glass plateDa convexo concave lensA convex lens made up of material of refractive index μ1, is immersed in a medium of refractive index μ2 as shown in the figure. The relation between μ1 and μ2 is
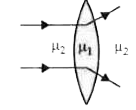 Aμ1<μ2Bμ1>μ2Cμ1=μ2Dμ1=√μ2
Aμ1<μ2Bμ1>μ2Cμ1=μ2Dμ1=√μ2
A right angled triangular prism of refractive index μ1 is kept floating on a liquid (surface) having refractive index μ2. The condition such tat light incident normally passes through base of prism as shown in figure.Aμ1=Cos2θ/CosθBμ2=Cos2θ/CosθCμ1=Sin2θ/CosθDμ2=Sin2θ/Sinθ
Statement-1 : A glass convex lens (refractive index, μ1=1.5), when immersed in a liquid of refractive index μ2=2, functions as a diverging lens.
Statement-2 : The focal length of a lens is given by 1f=(μ−1)(1R1−1R2), where μ is the relative refractive index of the material of the lens with respect to the surrounding medium.
View SolutionDetermine the value of the angle of incidence for a ray of light travelling from a medium of refractive index μ1=√2 into the medium of refractive index μ2=1, so that it just grazes along the surface of separation.
View SolutionAn equiconvex lens of refractive index μ2 is placed such that the refractive :
View SolutionA sphere of radius R made of material of refractive index μ2 is placed in a medium of refractive index μ1. Where would an object be placed so that a real image is formed at equidistant fromk the sphere? ltbgt
View SolutionA thin prism of angle 15∘ made of glass of refractive index μ1=1.5 is combined with another prism of glass of refractive index μ2=1.75. The combination of the prism produces dispersion without deviation. The angle of the second prism should be
View Solution
