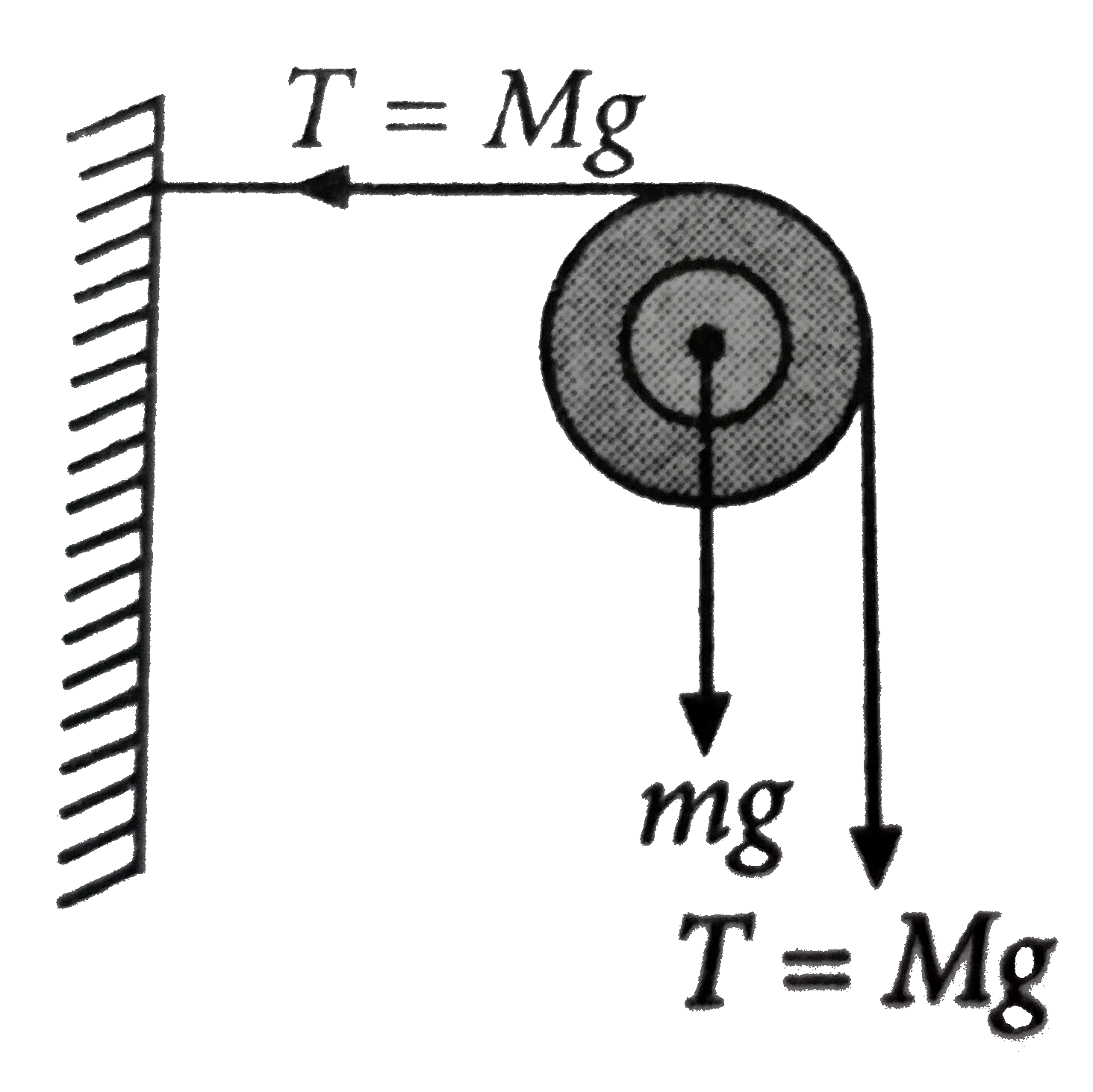
A string of negligible mass going over a clamped pulley of mass m supports a block of mass M as shown in the figure. The force on the pulley by the clamp is given by

The correct Answer is:D
Weight of the pulley mg acts downwards. Weight of the block Mg acts downwards. Total downward force.
Tension in the string T=Mg.
The force on the pulley by reaction of the clamp is equal to the resultant of and T. Let it be F.
Topper's Solved these Questions
- LAWS OF MOTIONBook:NCERT FINGERTIPSChapter:LAWS OF MOTIONExercise:NCERT Exemplar
Explore 9 Videos
- LAWS OF MOTIONBook:NCERT FINGERTIPSChapter:LAWS OF MOTIONExercise:Assertion And Reason
Explore 15 Videos
- LAWS OF MOTIONBook:NCERT FINGERTIPSChapter:LAWS OF MOTIONExercise:Solving Problem In Mechanics
Explore 16 Videos
- KINETIC THEORYBook:NCERT FINGERTIPSChapter:KINETIC THEORYExercise:Assertion And Reason
Explore 10 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NCERT FINGERTIPSChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Assertion And Reason
Explore 15 Videos
Similar Questions
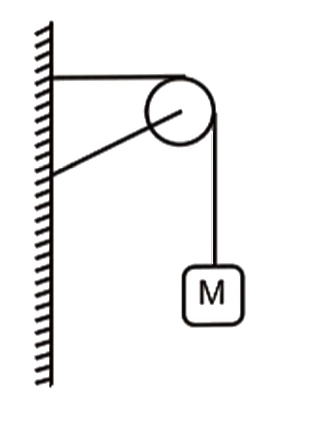
A mass string going over a clamped pulley of mass m supports a block of mass M as shown in the figure. The force on the pulley by the clamp is given
View SolutionA block of mass m hangs by means of a string which goes over a pulley of mass m and moment of inertia l, as shown in the diagram. The string does not relative to the pulley. Find the frequency of small oscillations.
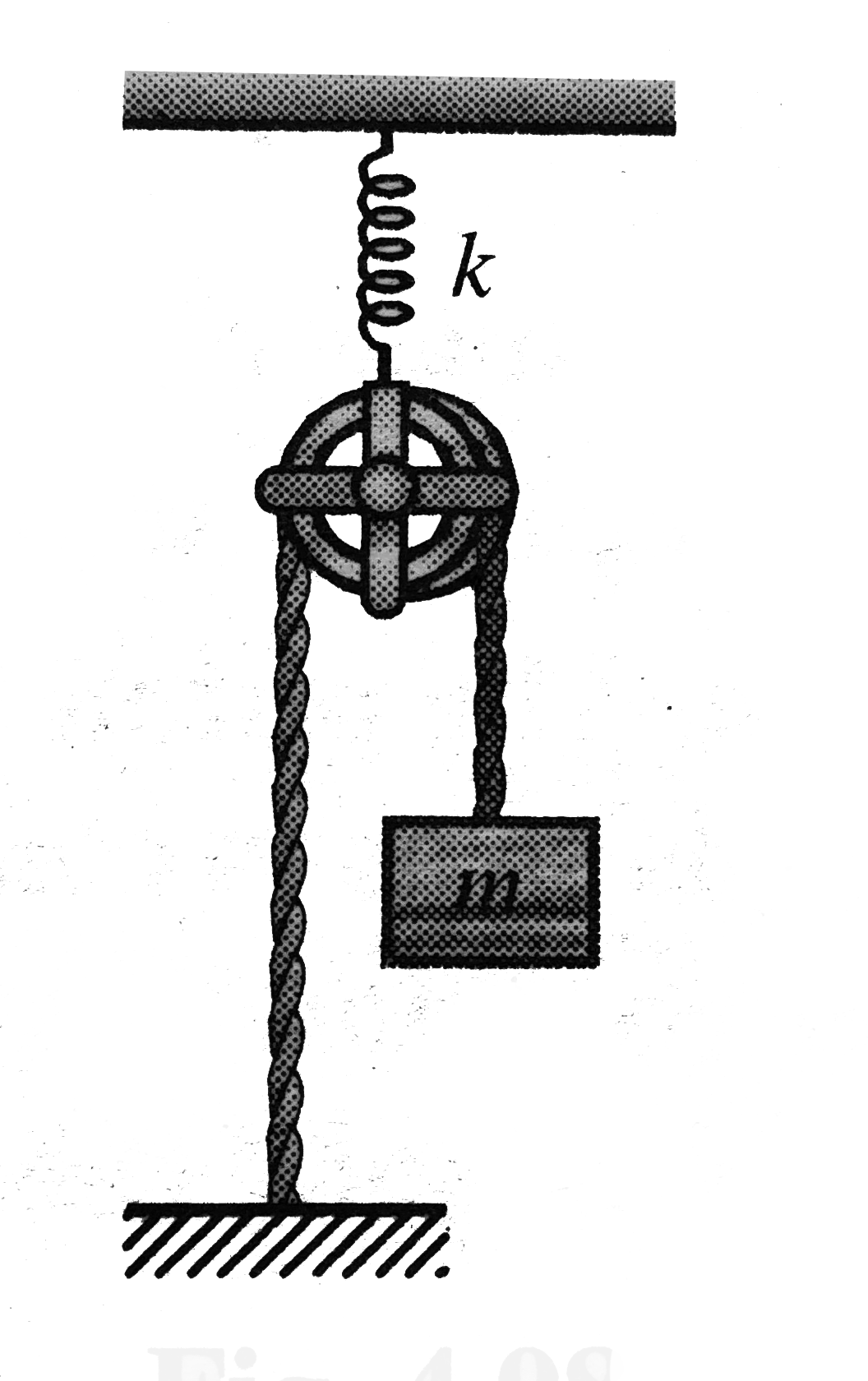
View Solution
Knowledge Check
A string of negligible mass going over a clamped puley of mass m supports a block of mass Mas shown in the figure. The force on the pulley by the clamp is given
 A√2 MgB√2 mgC√(M+m)2+m2gD√(M+m)2+M2g
A√2 MgB√2 mgC√(M+m)2+m2gD√(M+m)2+M2gA spring of negligible mass going over a clamped pulley of mass m supports a block of mass M as shown in the figure. The force on the pulley by the clamp at the time of equilibrium is given by
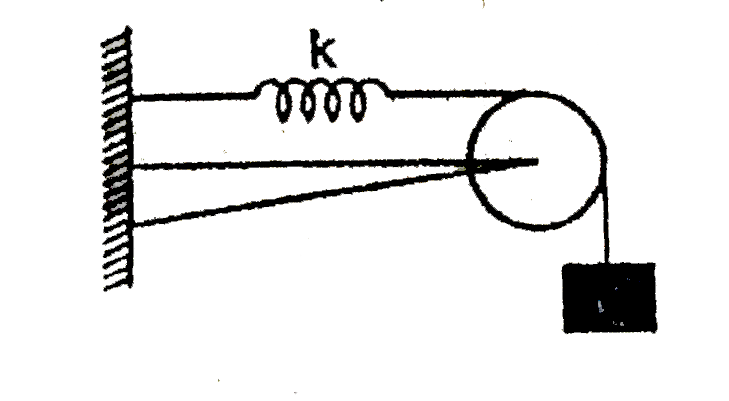 A√2MgB√(mg)2+(kx)2C(√(M+m)2+m2)gD(√(M+m)2+M2)g
A√2MgB√(mg)2+(kx)2C(√(M+m)2+m2)gD(√(M+m)2+M2)gTwo blocks of masses M1=4 kg and M2=6kg are connected by a string of negligible mass passing over a frictionless pulley as shown in the figure below. The coefficient of friction between the block M1 and the horizontal surface is 0.4. when the system is released, the masses M1 and M2 start accelrating. What additional mass m should be placed over M1 so that the masses (M1+m) slide with a uniform speed?
 A12 kgB11 kgC10 kgDkg
A12 kgB11 kgC10 kgDkg
Two blocks of masses 2m and m are connected by a light string going over a pulley of mass 2m and radius R as shown in the figure. The system is released from rest. Find the angular momentum of system when the mass 2m has descended through a height h. Assume no slipping.

View SolutionA constant force F=m_2g/sisappliedontheblockofmassm_1asshown∈figure.Thestr∈gandthep≤––––yarelightandthesurfaceofthetab≤issm∞th.F∈dtheae≤rationofm_1
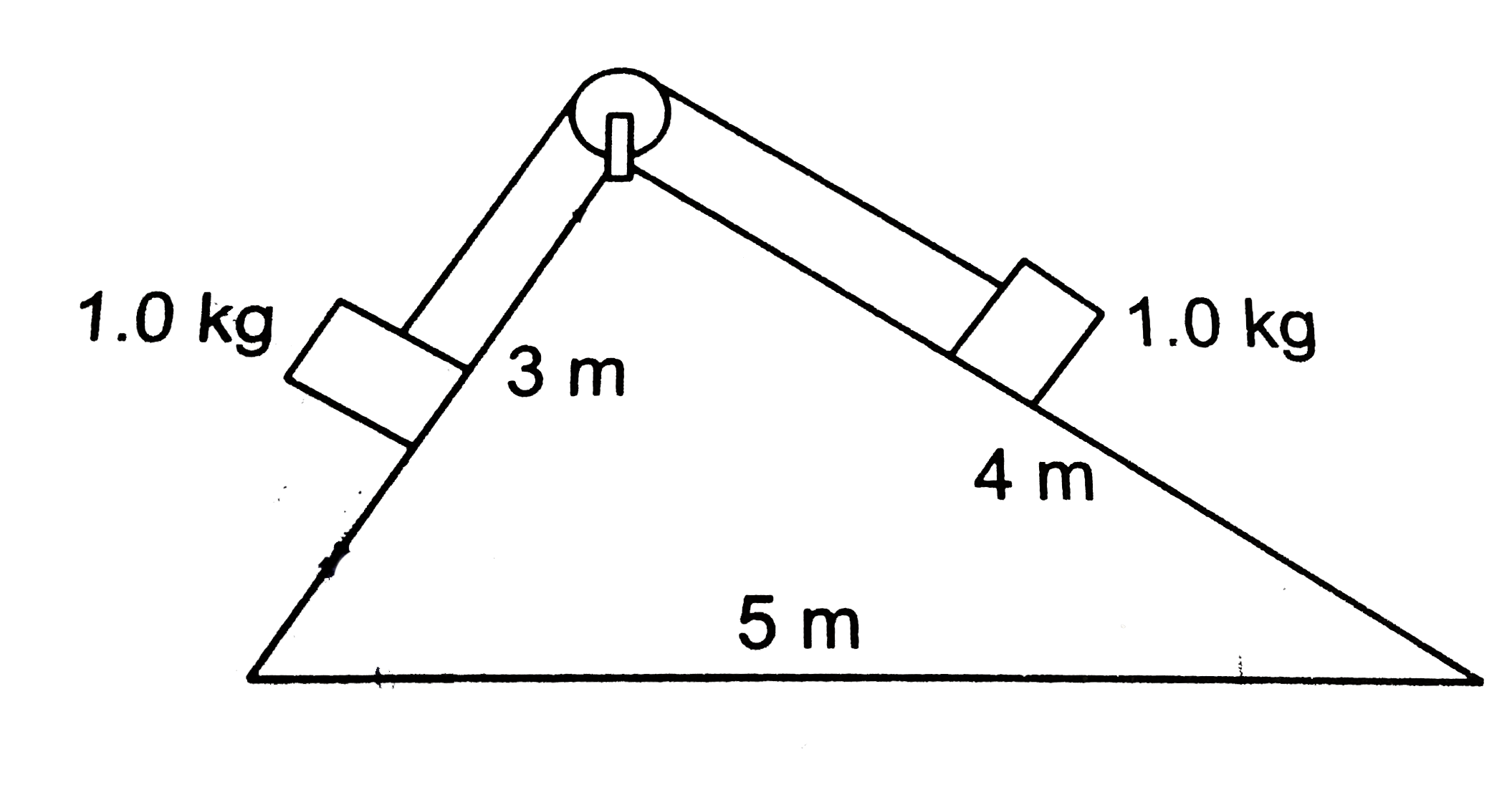
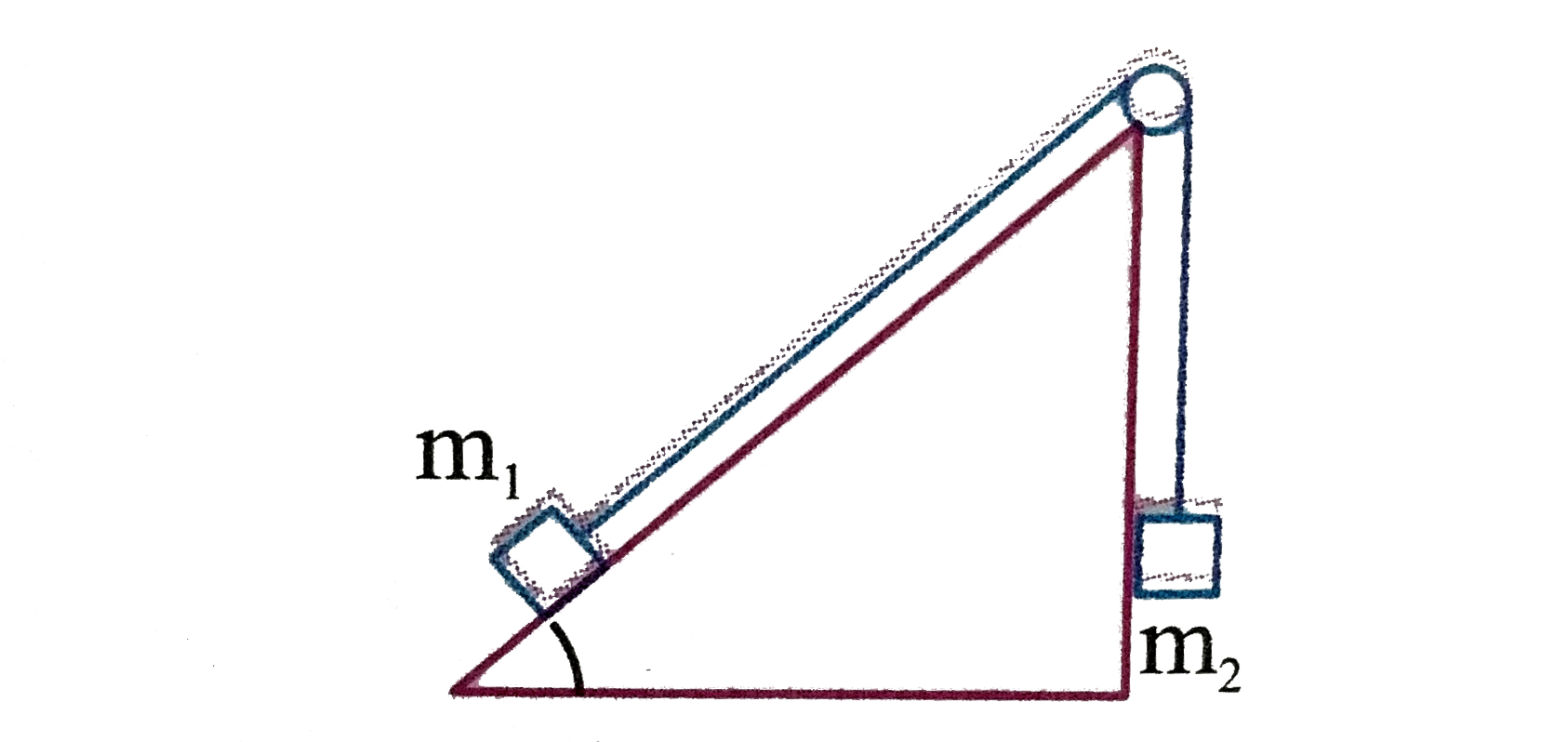
View SolutionTwo blocks of masses m1 and m2 are connected by a string of negligible mass which pass over a frictionless pulley fixed on the top of an inclined plane as shown in figure. The coefficient of friction between m1 and plane is μ.
View SolutionA string of negligible mass is wrapped on a cylindrical pulley of mass M and radius R. The other end of string is tied to a bucket of mass m. If the pulley rotates about a horizontal axis then the tension in the string is :
View SolutionBoth the blocks shown in figure have same mass 'm'. All the pulley and strings are massiess.

View Solution

