gamma(1) gt gamma(2) gt gamma(4) gt gamma(3)

In gamma $(γ)$ decay
ABoth a and Z increase by 1
BBoth A and Z decrease by 1
CNeither A nor Z changes
DA is always equal to Z
The coefficient of real expansion of liquid is $γ_{R}$ and the coefficient of appareent expansion of the liquid is $γ_{A}$ . The coefficient of cubical expansion of the vessel is $γ$ . If $γ_{R} : γ_{A} = 4 : 1$ then $γ_{A} : γ$ is
A $3 : 1$
B $1 : 3$
C $4 : 1$
D $1 : 4$
Gold nucleus $(_{79}^{198} A u)$ can decay into mercuyr nucleus $(_{80}^{198} H g^{8})$ by two decay schemes shown in figure below (i) it can emit a $β$ -particle $(β_{1})$ and come to ground state by either emiting one $γ$ - ray ( $γ_{1}$ ) or emitting two $γ$ - rays ( $γ_{3}$ and $γ_{4}$ ) (ii) It can emit one $β$ - particle $(β_{2})$ and come to ground state by emitting $γ_{2}$ ray. Atomic masses: $^{198} A u = 197.9652$ amu and $^{198} H g = 197.9662$ amu. Given that 1 amu= $930 M e V / c^{2}$ . The energy levels of the nucleus are shown in figure below

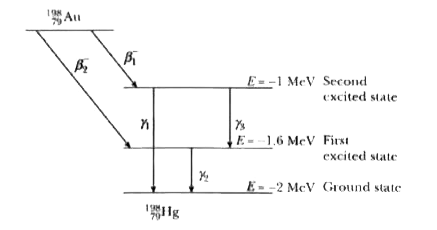
The wavelength of emitted $γ$ - rays is the order
A $λ_{2} > λ_{3} > λ_{1}$
B $λ_{3} > λ_{2} > λ_{1}$
C $λ_{1} > λ_{2} > λ_{3}$
D $λ_{3} = λ_{2} = λ_{1}$

Order of no. of revolutions/sec $γ_{1}, γ_{2}, γ_{3}$ and $γ_{4}$ for I, II, III and IV orbits is: