A rod of length I leans by its upper end against a smooth vertical wall, while its other end leans against the floor. The end that leans against the wall moves uniformly downward. Then:
The speed of lower end increases at a constant rate
The speed of the lower end decreases but never becomes zero
The speed of the lower and gets smaller and smaller and vanishes when the upper end touches the ground
The speed of the lower end remain constant till upper end touches the ground
The correct Answer is:C
Step by step video & text solution for A rod of length I leans by its upper end against a smooth vertical wall, while its other end leans against the floor. The end that leans against the wall moves uniformly downward. Then: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A rod of length 'l' is inclined at an angle 'θ' with the floor against a smooth vertical wall. If the end A moves instantaneously with velocity v1, what is the velocity of end B at the instant when rod makes 'θ' angle with the horizontal.
View SolutionA rod of length 'l' is inclined at an angle 'theta' with the floor against a smooth vertical wall. If the end A moves instantaneously with velocity v1 what is the velocity of end B at the instant when rod makes 'theta' angle with the horizontal .
View Solution
Knowledge Check
If a ladder is not in balance against a smooth vertical wall, then it can be made in balance by :-
ADecreasing the length of ladderBIncreasing the length of ladderCIncreasing the angle of inclinationDDecreasing the angle of inclinationA uniform rod AB of length a hangs with one end against a smooth vertical wall, being supported by a string of length l, attached to the other end of the rod and to a point of the rod vertically above B. If the rod rests inclined to the wall at angle θ then cos2θ=
A(l2−a2)/a2B(l2−a2)/2a2C(l2−a2)/3a2Dnone of theseA uniform ladder rests in limiting equilibrium, its lower end on a rough horizontal plae and its upper end against a smooth vertical wall. If θ is the engle of inclination of the ladder to the vertical wall and μ is the coefficient of friction then tanθ is equal to
AμB2μC3μ/2Dμ+1
A uniform ladder of length 3.25 m and weight 250 N is placed against a smooth vertical wall with its lower end 1.25 m from the wall. If coefficient of friction between the ladder and the floor is 0.3, then, find the frictional force acting on the ladder at the point of contact between ladder and floor.
View SolutionA light stick of length l rests with its one end against the smooth wall and other end against the smooth horizontal floor as shown in the figure. The bug starts at rest from point B and moves such that the stick always remains at rest. aP is the magnitude of acceleration of but of mass m, which depends upon its distance of x from the top end of the stick. Choose the correct option (s)
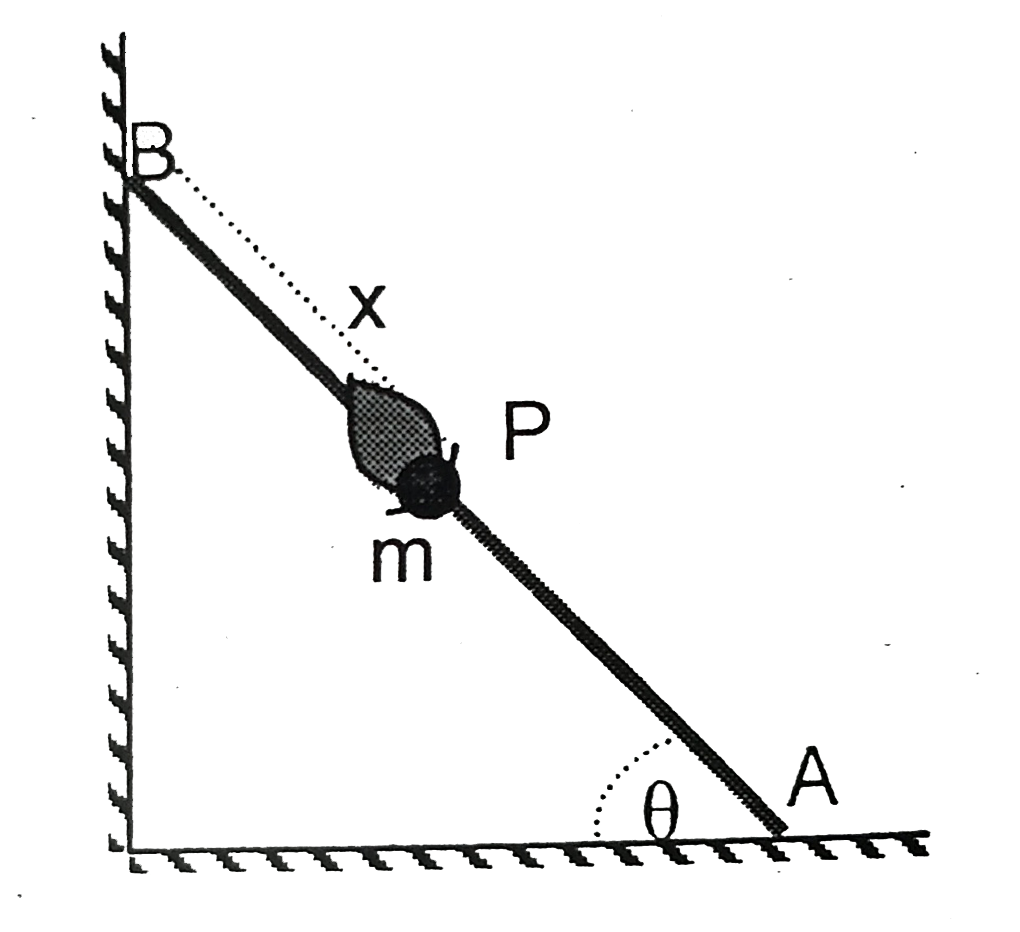
View SolutionA ladder 20 ft long leans against a vertical wall. The top end slides downwards at the rate of 2 ft per second. The rate at which the lower and moves on a horizontal floor when it is 12 ft from the wall is
View SolutionA uniform ladder rests in limiting equilibrium with its lower end on a rough horizontal plane with coefficient of friction μ and its upper end against a smooth vertical wall. If θ is the inclination of the ladder with the wall, then θ is equal to
View SolutionA uniform ladder rests in limiting equilibrium with its lower end on a rough horizontal plane with coefficient of friction μ and its upper end against a smooth vertical wall. If θ is the inclination of the ladder with the wall, then θ is equal to
View Solution
