A stationary uniform rod of mass 'm', length 'l' leans against a smooth vertical wall making an angle θ with horizontal floor. Find the normal force & frictional force that is exerted by the floor on the rod ?
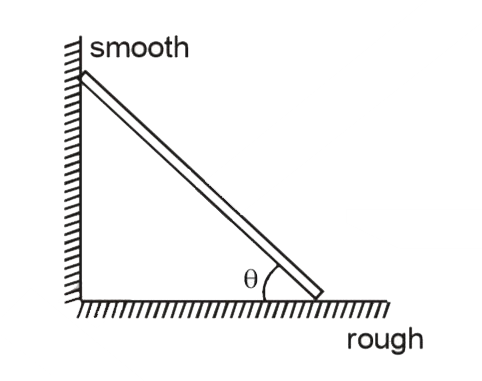
As the rod is stationary so the linear acceleration and angular acceleration of rod is zero.
i.e., acm=0,α=0
N2=fN1=mg}∵aam=0
Torque about any point of the rod should also be zero
∴α=0
τA=0⇒mgcosθl2+flsinθ=N1cosθ.l
N1cosθ=sinθf+mgcosθ2
f=mgcosθ2sinθ=mgcotθ2

Topper's Solved these Questions
Similar Questions
A uniform ladder of mass 10 kg leans against a smooth vertical wall making an angle of 530 with it. The other end rests on a rough horizontal floor. Find the normal force and the frictional force that the floor exerts on the ladder
View SolutionThe moment of inertia of a thin uniform rod of mass M, length L, about an axis passing through its centre and making an angle θ with the rod is
View Solution
Knowledge Check
A rod of mass m is released on smooth horizontal surface making angle θ with horizontal. Then which of the following statement is correct ?
AAcceleration of rod along vertical is less than gBAcceleration of centre of mass along horizontal is zero.CAngular acceleration of rod is not constantDMomentum of the rod along vertical will remain constant
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:A12mVLcosθB13mVLsinθCmVLsincosθDzeroIn the figure, a ladder of mass m is shown leaning against a wall. It is in static equilibrium making an angle θ with the horizontal floor. The coefficient of friction between the wall and the ladder is μ1 and that between the floor and the ladder is μ2. the normal reaction of the wall on the ladder is N1 and that of the floor is N2. if the ladder is about to slip. than
 Aμ1=0,μ2≠andN2tanθ=mg2Bμ1≠0,μ2=0andN1tanθ=mg2Cμ1≠0,μ2≠0andN2=mg1+μ1μ2Dμ1=0,μ2≠0andN1tanθ=mg2
Aμ1=0,μ2≠andN2tanθ=mg2Bμ1≠0,μ2=0andN1tanθ=mg2Cμ1≠0,μ2≠0andN2=mg1+μ1μ2Dμ1=0,μ2≠0andN1tanθ=mg2
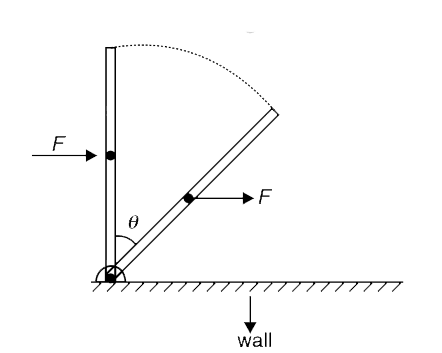
A uniform rod of mass M and length L is hinged at its end to a wall so that it can rotate freely in a horizontal plane. When the rod is perpendicular to the wall a constant force F starts acting at the centre of the rod in a horizontal direction perpendicular to the rod. The force remains parallel to its original direction and acts at the centre of the rod as the rod rotates. (Neglect gravity).
(a) With what angular speed will the rod hit the wall ?
(b) At what angle θ (see figure) the hinge force will make a 45∘ angle with the rod ?
View SolutionA uniform rod of length 1m having mass 1kg rests against a smooth wall at an angle of 30∘ with the ground. Calculate the force exerted by the ground on the rod. Take g=10ms−2.
View SolutionA uniform thin rod of mass m and length R is placed normally on surface of earth as shown. The mass of earth is M and its radius R. Then the magnitude of gravitational force exerted by earth on the rod is

View SolutionA uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
View SolutionA ball of mass m=1kg strikes a smooth horizontal floor as shown in figure. The impulse exerted on the floor is

View Solution
