A particle of mass m is projected with velocity v at an angle θ with the horizontal. Find its angular momentum about the point of projection when it is at the highest point of its trajectory.
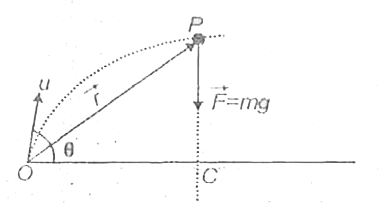
As shown in the figure, required torque →τ=→r×→F.
But as it is the product of force and the length of perpendicular OC drawn from the point of projection on the line of action of the force.
Here, OC=Range2
=2u2sinθ.cosθ2g
So, torque = (Force) × (OC)
=mg(2u2sinθ.cosθ2g)
=μ2sinθ.cosθ
Similar Questions
A body of mass m is projected with a velocity u at an angle θ with the horizontal. The angular momentum of the body, about the point of projection, when it at highest point on its trajectory is
View SolutionA particle of mass m is thrown with speed v0 at angle 30∘ with horizontal. Find the angular momentum about the point of projection when the particle is at the highest point of its trajectory.
View Solution
Knowledge Check
A particle of mass m is projected with a velocity μ at an angle of θ with horizontal.The angular momentum of the particle about the highest point of its trajectory is equal to :
Amu3sin2θcosθ3gB3mu3sin2θcosθ3gCmu3sin2θcosθ2gD2mu3sinθcos2θ3gA particle of mass m is projected with a velocity v making an angle of 45° with the horizontal. The magnitude of the angular momentum of the projectile about the point of projection, when the particle is at its maximum height h, is
AzeroBmv34√2gCmv3√2gDm√2gh3A particle of mass m is projected with a velocity v making an angle of 45∘ with the horizontal. The magnitude of the angular momentum of the projectile abut the point of projection when the particle is at its maximum height h is.
AzeroB(mv)34√2gC(mv)3√2gDm√2gh3
A particle of mass m is projected with a speed u at an angle θ with the horizontal. Find angular momentum of particle after time t about point of projection.
View SolutionA body of mass m is projected with velocity v at an angle of 45∘ with the horizontal. Find the change in its momentum at the end of flight.
View SolutionA particle of mass m is projected with a speed u at an angle θ to the horizontal at time t=0. Find its angular momentum about the point of projection O at time t, vectorially. Assume the horizontal and vertical lines through O as X and Y axes, respectively.
View SolutionA particle of mass m is projected with a speed v at an angle θ with the horizontal. Find the angular momentum of the particle about an axis passing through point of projection and perpendicular to the plane of motion of the particle.
(a) When the particle is at maximum height and
(b) When the particle is just about to collide with the horizontal surface
View SolutionA particle of mass m is projecte dwilth speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View Solution
