A disc of radius r is cut from a larger disc of radius 4r in such a way that the edge of the hole touches the edge of the disc. The centre of mass of the residual disc will be a distance from centre of larger disc :-
Method - I : Figure shows the point C as the centre of the whole disc. C1 is the centre of the hole and C2 is the centre of mass of the residual disc. If m be the mass of the disc cut from the larger disc, then mass of the whole disc is 16 m, because mass of a disc varies as the square of its radius.
So, the mass of the residual is m2=16m−m=15m
Clearly, C is the centre of mass of two masses m1=m and m2=15m at C1 and C2 respectively, where CC1=4r−r=3r=x1 (say). Let CC2=x2. If we take C as the origin, then xcm=0.
Now using xcm=m1x1+m2x2m1+m2, we get 0=m1x1+m2(−x2)m1+m2
or, m1x1=m2x2, Remember as formula
so, x2=m1x1m2=(m)(3r)(15m)=r5
i.e., CC2=r5
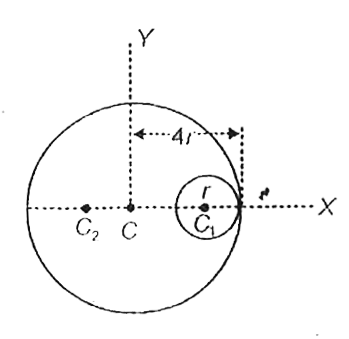
Method - II : We may also use formula xCM=x1A1−x2A2A1−A2
Here A1=16πr2,A2=πr2
x1=0 and x2=3r
∴xCM=0−3r−πr216πr2−πr2=−r5
∴CC2=r5
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Illustration
4 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)
62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTECHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTECHAPTER - TEST 1EXERCISE - EXERCISE
9 Videos
Similar Questions
A disc of radis R is cut out from a larger disc of radius 2R in such a way that the edge of the hole touches the edge of the disc. Locate the centre of mass of the residual disc.
View SolutionA circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is
View Solution
Knowledge Check
A circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is
A335cmB135cmC310cmDNone of theseA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumference of the discs coincoid . The centre of mass of the new disc is αR from the centre of the bigger disc . the value of α is
A1/3B1/2C1/6D1/4A circular disc of radius R is removed from a bigger circular disc of radius 2R such that the cirucmferences of the discs coincide. The centre of mass of the new disc is αR from the center of the bigger disc. The value of α is
A14B13C12D16
A circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumference of the discs coincoid . The centre of mass of the new disc is αR from the centre of the bigger disc . the value of α is
View SolutionA circular disc of radius R is removed from a bigger circular dise of radius such that the circumferences of the discs coincide. The centre of mass of the new disc is αR from the centre of the bigger disc. The value of a is:
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumferences of the discs coincide. The center of mass of new disc is αR from the center of the bigger disc. The value of α is
View SolutionA small disc of radius 2cm is cut from a disc of radius 6cm. If the distance their centers is 3.2cm, what is the shift in the center of mass of the disc?
View SolutionGiven a uniform disc of mass M and radius R. A small disc of radius R/2 is cut from this disc in such a way that the distance between the centres of the two discs is R/2. Find the moment of inertia of the remaining disc about a diameter of the original disc perpendicular to the line connecting the centres of the two discs
View Solution
