When a particle is thrown vertically upwards, its velocity at one third of its maximum height is . The maximum height attained by it is
15 m
12.8 m
The correct Answer is:C
To solve the problem, we will use the equations of motion under uniform acceleration. Here’s the step-by-step solution:
Step 1: Understand the problem
We have a particle thrown vertically upwards, and we know its velocity at one-third of its maximum height. We need to find the maximum height attained by the particle.
Step 2: Define variables
Let:
- Hmax = maximum height attained by the particle
- v = velocity at one-third of the maximum height = 10√2m/s
- g = acceleration due to gravity = 9.81m/s2 (approximately 10m/s2 for simplicity)
Step 3: Use the kinematic equation
We can use the kinematic equation that relates initial velocity, final velocity, acceleration, and displacement:
v2=u2−2gh
where:
- v = final velocity at height Hmax3
- u = initial velocity (which we will express in terms of Hmax)
- h = height = Hmax3
Step 4: Substitute known values
At height Hmax3:
(10√2)2=u2−2g(Hmax3)
Calculating (10√2)2:
200=u2−2gHmax3
Step 5: Express initial velocity u
From the equation for maximum height, we know:
Hmax=u22g
Thus, we can express u2 in terms of Hmax:
u2=2gHmax
Step 6: Substitute u2 into the equation
Substituting u2 into our earlier equation:
200=2gHmax−2gHmax3
Combining the terms:
200=2gHmax(1−13)=2gHmax(23)
This simplifies to:
200=4gHmax3
Step 7: Solve for Hmax
Rearranging gives:
Hmax=200×34g
Substituting g≈10m/s2:
Hmax=60040=15m
Final Answer
The maximum height attained by the particle is Hmax=15m.
---
We have a particle thrown vertically upwards, and we know its velocity at one-third of its maximum height. We need to find the maximum height attained by the particle.
Let:
- Hmax = maximum height attained by the particle
- v = velocity at one-third of the maximum height = 10√2m/s
- g = acceleration due to gravity = 9.81m/s2 (approximately 10m/s2 for simplicity)
We can use the kinematic equation that relates initial velocity, final velocity, acceleration, and displacement:
v2=u2−2gh
where:
- v = final velocity at height Hmax3
- u = initial velocity (which we will express in terms of Hmax)
- h = height = Hmax3
At height Hmax3:
(10√2)2=u2−2g(Hmax3)
Calculating (10√2)2:
200=u2−2gHmax3
From the equation for maximum height, we know:
Hmax=u22g
Thus, we can express u2 in terms of Hmax:
u2=2gHmax
Substituting u2 into our earlier equation:
200=2gHmax−2gHmax3
Combining the terms:
200=2gHmax(1−13)=2gHmax(23)
This simplifies to:
200=4gHmax3
Rearranging gives:
Hmax=200×34g
Substituting g≈10m/s2:
Hmax=60040=15m
The maximum height attained by the particle is Hmax=15m.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - C)
Explore 37 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - D)
Explore 15 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - A)
Explore 60 Videos
- MOTION IN A PLANEBook:AAKASH INSTITUTEChapter:MOTION IN A PLANEExercise:Assignement section -J (Aakash Challengers Questions)
Explore 4 Videos
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN STRAIGHT LINEExercise:Assignment (SECTION - J)
Explore 2 Videos
Similar Questions
When a ball is thrown vertically upwards, at the maximum height
View SolutionA particle is thrown vertically upward with speed 40m/s.
(a) After how much time attains maximum height?
(b) Find (i) the maximum height attained by the particle.
(ii) the velocity at half of the maximum height.
(c ) Find (i) the ratio of distances in the first half and the next half of time.
the ratio of the time in the first half and the second half of the distance (consider only upward journey)
View Solution
Knowledge Check
A particle is thrown vertically upwards. If its velocity is half of the maximum height is 20m/s, then maximum height attained by it is
A25 mB30 mC35 mD40 mA particle is thrown vertically upward. Its velocity at half of the height is 10 m/s. Then the maximum height attained by it : -
(g=10m/s2)A8 mB20 mC10 mD16 mA stone is thrown vertically upwards. When stone is at a height half of its maximum height, its speed is 10ms−1 , then the maximum height attained by the stone is (g=10ms−2)
A25 mB10 mC15 mD20 m
A stone is projected vertically upwards.When it reaches half the maximum height,its velocity is 20m/s.What is the maximum height attained by the stone? (g=10m/s^(2)
View SolutionA ball is thrown vertically upward with a velocity of 20 m/s. Calculate the maximum height attain by the ball.
View SolutionA rocket is projected vertically upwards and its time velocity graph is shown in the figure-1.115. The maximum height attained by the rocket is :
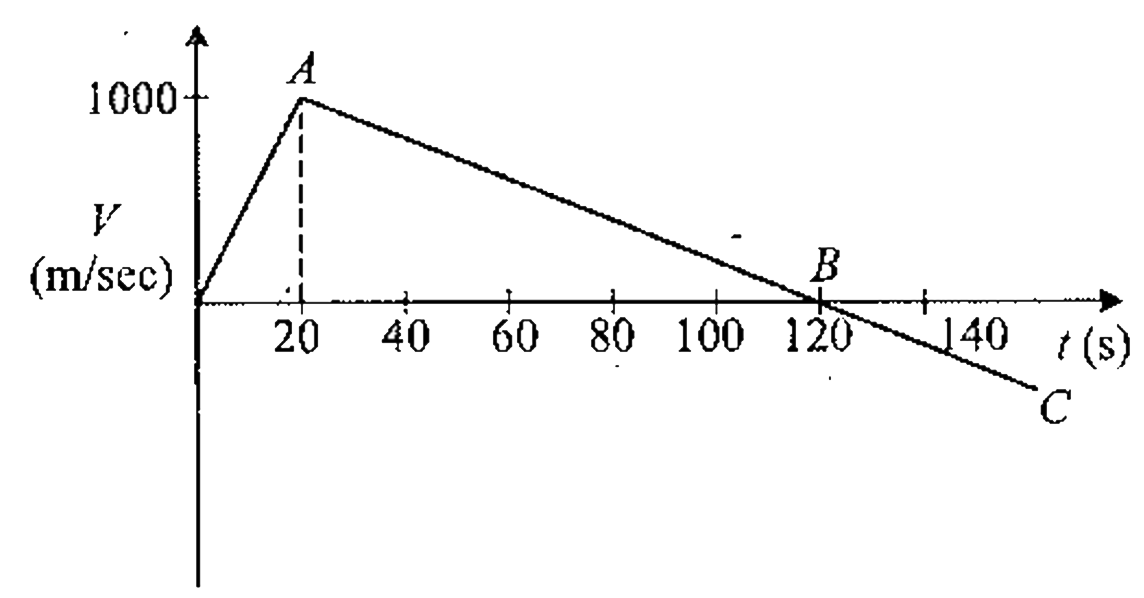
View SolutionA ball is thrown vertically upward in air. When the particle is at a height half of its maximum height its speed is 10 m/s. Then the maximum height attained by the particle is
View SolutionA particle is thrown vertically upward from the ground with some velocity and it strikes the ground again in time 2 s. The maximum height achieved by the particle is : (g=10m/s2)
View Solution

