A solid insulating sphere of radius R is given a charge Q. If at a point inside the sphere the potential is 1.5 times the potential at the surface, this point will be
at a distance of 2R/3 from the centre
at the centre
at a distance of 2R/3 from the surface
data insufficient
The correct Answer is:B
To solve the problem, we need to find the point inside a solid insulating sphere of radius R where the electric potential is 1.5 times the potential at the surface of the sphere. Let's break down the solution step by step.
Step 1: Understand the potential inside and on the surface of the sphere
The potential V at a distance r from the center of a uniformly charged solid insulating sphere of radius R and total charge Q is given by:
V(r)=kQ2R(3−r2R2)for r≤R
where k is Coulomb's constant.
The potential at the surface of the sphere (when r=R) is:
V(R)=kQR
Step 2: Set up the equation based on the given condition
According to the problem, the potential at a point inside the sphere is 1.5 times the potential at the surface. Therefore, we can write:
V(r)=1.5×V(R)
Substituting the expression for V(R):
V(r)=1.5×kQR
Step 3: Equate the two expressions for potential
Now, we can set the two expressions for potential equal to each other:
kQ2R(3−r2R2)=1.5×kQR
Step 4: Simplify the equation
We can cancel kQ from both sides (assuming kQ≠0):
12R(3−r2R2)=1.5
Multiplying both sides by 2R:
3−r2R2=3R
Step 5: Solve for r2
Rearranging the equation gives:
−r2R2=3R−3
Multiplying through by -1:
r2R2=3−3R
Step 6: Find the value of r
Now, we can express r2:
r2=R2(3−3R)
To find r, we take the square root:
r=R√3−3R
Step 7: Determine the point inside the sphere
Since R is the radius of the sphere, the only valid solution for r must be less than or equal to R. The only point where the potential is 1.5 times the surface potential occurs at the center of the sphere when R=0.
Conclusion
Thus, the point inside the sphere where the potential is 1.5 times the potential at the surface is at the center of the sphere.
Final Answer: The point will be at the center of the sphere.
---
The potential V at a distance r from the center of a uniformly charged solid insulating sphere of radius R and total charge Q is given by:
According to the problem, the potential at a point inside the sphere is 1.5 times the potential at the surface. Therefore, we can write:
Now, we can set the two expressions for potential equal to each other:
We can cancel kQ from both sides (assuming kQ≠0):
Rearranging the equation gives:
Now, we can express r2:
Since R is the radius of the sphere, the only valid solution for r must be less than or equal to R. The only point where the potential is 1.5 times the surface potential occurs at the center of the sphere when R=0.
Thus, the point inside the sphere where the potential is 1.5 times the potential at the surface is at the center of the sphere.
Topper's Solved these Questions
- ELECTROSTANTICSBook:FIITJEEChapter:ELECTROSTANTICSExercise:ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL - II
Explore 13 Videos
- ELECTROSTANTICSBook:FIITJEEChapter:ELECTROSTANTICSExercise:COMPREHENSION BASED (COMPREHENSION - II)
Explore 3 Videos
- ELECTROSTANTICSBook:FIITJEEChapter:ELECTROSTANTICSExercise:ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL - II & III
Explore 15 Videos
- ELECTROMAGNETIC WAVE & WAVE OPTICSBook:FIITJEEChapter:ELECTROMAGNETIC WAVE & WAVE OPTICSExercise:ASSIGNMENT PROBLEMS Objective : Level-II (MULTI CHOICE SINGLE CORRECT)
Explore 21 Videos
- ELECTROSTATICSBook:FIITJEEChapter:ELECTROSTATICSExercise:Example
Explore 14 Videos
Similar Questions
A solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :

View SolutionA non-conducting sphere of radius R is given a charge Q. Charge is uniformly distributed in its volume. The electric potential at centre and at the surface of sphere respectively are
View Solution
Knowledge Check
A conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the centre of the sphere respectively are
AZero and Q4πε0R2BQ4πε0R2 and zeroCQ4πε0R and Q4πε0R2DBoth are zeroLet ρ(r)=QrπR4 be the charge density distribution for a solid sphere of radius R and total charge Q. For a point P inside the sphere at a distance r1 from the centre of the sphere, the magnitude of electric field is
AQr214πε0R4BQr213πε0R4C0DQ4iε0r21Let ρ(r)=QrπR4 be the charge density distribution for a solid sphere of radius R and total charge Q. For a point P inside the sphere at a distance r1 from the centre of the sphere, the magnitude of electric field is
AQ4πε0r21BQr214πε0R4CQr213πε0R4Dzero
A non-conducting sphere of radius R is given a charge Q. Charge is uniformly distributed in its volume. The electric potential at centre and at the surface of sphere respectively are
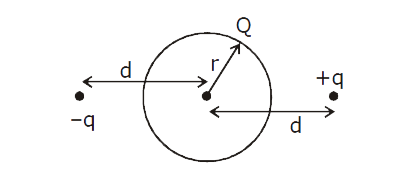
View SolutionA solid conducting sphere of radius r is having a charge Q and point charges +q and -q are kept at distance d from the centre of sphere as shown in the figure. The electric potential at the centre of solid sphere
(assume potential to be 0 at infinity)
View SolutionLet p(r)=QπR4r be the charge JIR density distribution for a solid sphere of radius R and total charge Q. For a point P inside the sphere at distance z1from the centre of the sphere, the magnitude of electric field is
View SolutionLet P(r)=QπR4r be the charge density distribution for a solid sphere of radius R and total charge Q. For a point 'p' inside the sphere at distance r1 from the centre of the sphere, the magnitude of electric field is:
View SolutionMetallic sphere of radius R is charged to potential V. Then charge q is proportional to
View Solution

