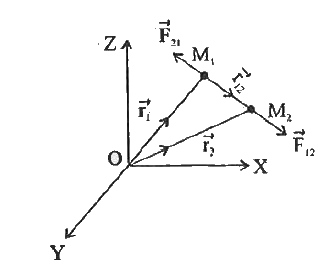
If →r1and→r2 are the position vectors of mass bodies M1andM2 then represent force between them in a vector from. Solution in Kannada
From the figure,
−→r12and→r2−→r1
By Newton's gravitational law ,
−→F12=−GM1M2r3.−→r12
i.e., −→F21=−Gm1m2r3.−→r21
where −→F21 is force on 2 due to 1
and −→r12=→r2−→r1and→r=xˆi+yˆj+zˆk
Topper's Solved these Questions
- GRAVITATION Book:SUBHASH PUBLICATIONChapter:GRAVITATION Exercise:FIVE MARKS QUESTIONS WITH ANSWERS
Explore 7 Videos
- GRAVITATION Book:SUBHASH PUBLICATIONChapter:GRAVITATION Exercise:NUMERICALS WITH SOLUTIONS
Explore 15 Videos
- GRAVITATION Book:SUBHASH PUBLICATIONChapter:GRAVITATION Exercise:TWO MARKS QUESTIONS WITH ANSWERS
Explore 5 Videos
- ANNUAL EXAMINATION QUESTION PAPER WITH ANSWER SOUTH 2019Book:SUBHASH PUBLICATIONChapter:ANNUAL EXAMINATION QUESTION PAPER WITH ANSWER SOUTH 2019Exercise:PART-D
Explore 9 Videos
- KINETIC THEORYBook:SUBHASH PUBLICATIONChapter:KINETIC THEORYExercise:NUMERICALS WITH SOLUTIONS
Explore 19 Videos
Similar Questions
State Kepler's law of planetary motion.
View SolutionAssuming the distance of the Moon from the Earth R=3.84×108m and Moon's period of revolution as 27.3 days, calculate the mass of the Moon.
View SolutionExplain why gravitational force is called a centre force ?
View SolutionState and explain parallel axis theorem and perpendicular axis theorem.
View SolutionIf atomic mass of Argon = 39.9 μ, molecular mass of chlorine = 70.9μ then find the ratio of r.m.s speed of argon atom and chlorine gas molecule.
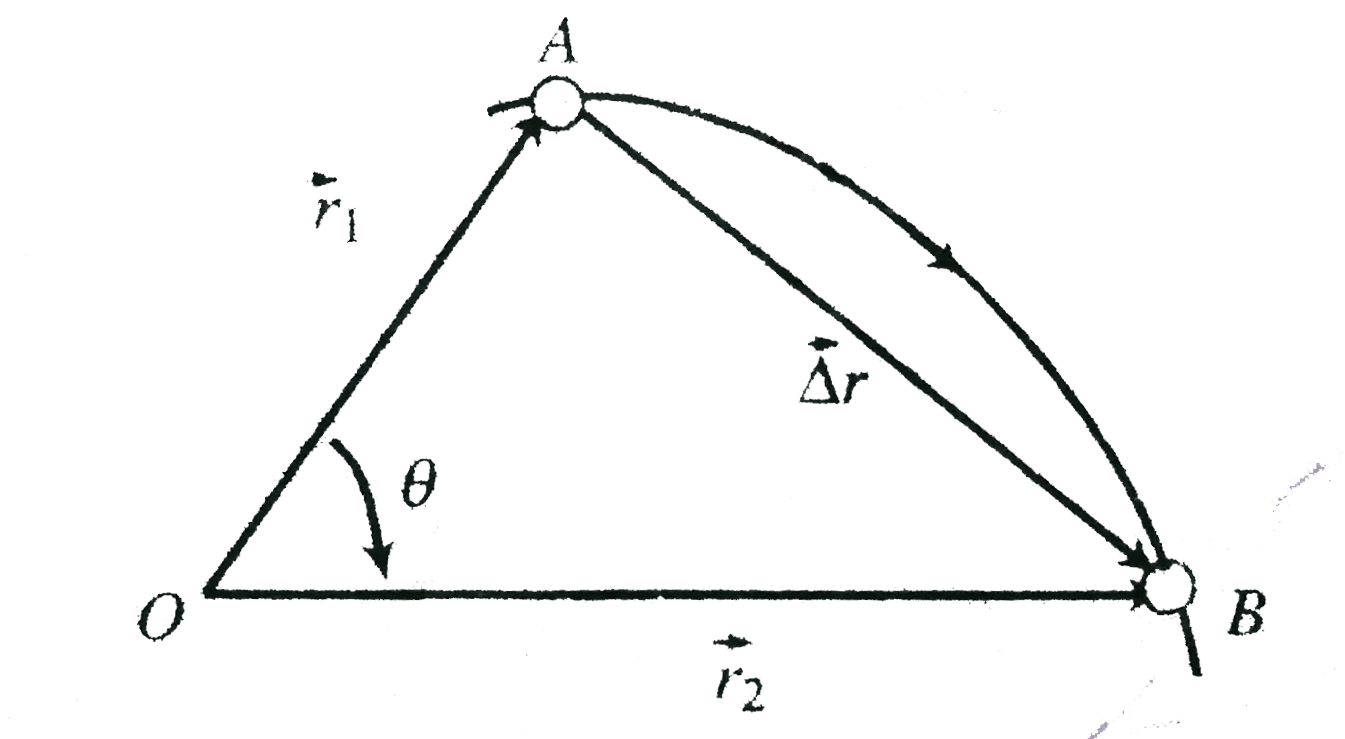
View SolutionA particle moves from position A to position B in a path as shown in If the poit vectors →r1 and →r2 making an angle θ between them are give, find the magnitude of displacement.
 .
.
View SolutionSupposing Newton's law of gravitation for gravitation force F1 and F2 between two masses m1 and m2 at positions r1 and r2 read F2=−F2=r12r312GM20(m1m2M20)n where M0 is a constant dimension of mass, r12=r1−r2 and n is number. In such a case.
View SolutionTwo concentric spherical shells have masses m_(1) and m_(2) and radii r_(1) and r_(2) (r_(2) gt r_(1)) . What is the force exerted by this system on a particle of mass m_(3) . If it is placed at a distance r(r_(1) lt r lt r_(2)) from the centre ?
View SolutionSupposing Newton's law of gravitation for gravitation forces F_(1) and F_(2) between two masses m_(1) and m_(2) at positions r_(1) and r_(2) read where M_(0) is a constant of dimension of mass, r_(12) = r_(1) - r_(2) and n is a number. In such a case,
View SolutionA particle has its position moved from vec(r_(1))=3hati+4hatj to vec(r_(2))=hati+2hatj . Calculate the displacment vector (Delta vecr) and draw the vec(r_(1)), vec(r_(2)) and Delta vecr vector in a two dimensional Cartesian coordinate system.
View Solutionद्रव्यमान केंद्र क्या है ? द्विकण निकाय के लिए सिद्ध कीजिए कि −−→rcm=m1→r1+m2→r2m1+m2
जहाँ संकेतों के सामान्य अर्थ हैं ।
View SolutionA force acting on a body displaces it from position vector →r1=(2ˆi−ˆj+3ˆk)m to →r2=(5ˆi−2ˆj+4ˆk)m. Then find the displacement vector.
View SolutionPosition vector of centre of two particles of masses m1 and m2 whose position vectors r1 and r2 then rcm?
View SolutionSupposing Newton's law of gravitation for gravitation forces F1 and F2 between two masses m1 and m2 at positions r1 and r2 read
where M0 is a constant of dimension of mass, r12=r1−r2 and n is a number. In such a case,
View SolutionThe distance between two particles of masses m1andm2 is r. If the distance of these particles from the centre of mass of the system are r1andr2 respectively, then show that r1=r(m2m1+m2)andr2=r(m1m1+m2)
View Solution

