Suppose A is a $3 \times 3$ matrix consisting of integer entries that are chosen at random from the set ${- 1000, 999, \dots ., 999, 1000}$ . Let P be the probability that either $A^{2} = - I$ or A is diagonal, where I is the $3 \times 3$ identity matrix. Then

A

$P < \frac{1}{10^{18}}$

B

$P = \frac{1}{10^{18}}$

C

$\frac{5^{2}}{10^{18}} \leq P \leq \frac{5^{3}}{10^{18}}$

D

$P > \frac{5^{4}}{10^{18}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$A = {[]}_{3 \times 3}$
$A^{2} = - I$
Taking det
${| A |}^{2} = - 1$ (Not possible)
$A \to$ diagonal matrix

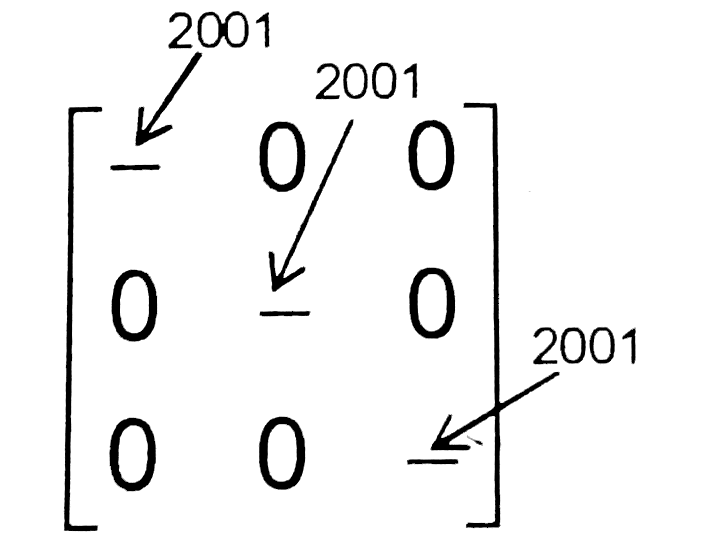
$P = \frac{{(2001)}^{3}}{{(2001)}^{9}} = \frac{1}{{(2001)}^{6}}$
$P = {(1 + 2000)}^{- 6}$
$= (2000^{- 6}) {(1 + \frac{1}{(2001)})}^{- 6} less than ⊥$
$= \frac{1}{2^{6} \times 10^{18}} (⏐ ↓)$
$P < \frac{1}{10^{18}}$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If a number n is chosen at random from the set {1,2,3,4,….,1000}. Then , the probability that n is a number that leaves remainder 1, when divided by 7, is
A $\frac{71}{500}$
B $\frac{143}{1000}$
C $\frac{72}{500}$
D $\frac{71}{1000}$
Question 2 - Select One
If for a $2 \times 2$ matrix $A, A^{2} + I = O$ , where I is identity matrix then A equals
A $[\begin{matrix} 1 & 0 0 & 1 \end{matrix}]$
B $[\begin{matrix} - i & 0 0 & - i \end{matrix}]$
C $[\begin{matrix} 1 & 2 - 1 & 1 \end{matrix}]$
D $[\begin{matrix} - 1 & 0 0 & - 1 \end{matrix}]$
Question 3 - Select One
If nine squares are chosen at random on a chess board, find the probability that they form a square of size $3 \times 3 .$
A $\frac{9}{^{64} C_{9}}$
B $\frac{36}{^{64} C_{9}}$
C $\frac{6}{^{64} C_{9}}$
Dnone of these

KVPY PREVIOUS YEAR-KVPY-PART-1 MATHEMATICS

Home
Ask Doubt
Profile