Proteins P,Q, and R are associated with intact organellar membrane in a cell. If the intact organelles is treated with a high ionic strength buffer, only protein R remained associated with the membrane fraction. Based on this, one could conclude that
P and Q are per peripheral membrane protein
R is a peripheral membrane protein
P and Q are integral membrane bound proteins.
P is peripheral and Q is integral membrane protein.
The correct Answer is:A
Peripheral proteins can be detached earily.
Topper's Solved these Questions
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Part 1 Biology
46 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Part 2 Biology
12 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Part A -Biology
20 Videos
- KVPY 2021BOOK - KVPY PREVIOUS YEARCHAPTER - KVPY 2021EXERCISE - PART I BIOLOGY
19 Videos
Similar Questions
There are five animals P, Q, R, S and T. The animal P always lives in water and has gills for breathing. The animal Q can saty in water as well as on land and can breathe both, through moist skin and lungs. The animal R lives in soil and breathes only through its skin. The animal S lives on land and breathes through spiracles and tracheae. And animal T lives in water and breathes through its cell membrane.
(a) Which of the animals could be Amoeba ?
(b) Which of the animals could be frog ?
(c) Which animal could be fish ?
(d) Which animal could be grasshopper?
(e) Which animal could be earthworm ?
View SolutionIn the following items, each passage consists of six sentences. The first and the sixth sentence are given in the beginning as S1 and 56. The middle four sentences in each have been removed and jumbled up. These are labelled P, Q, R and S. You are required to find out the proper sequence of the four sentences and mark your response accordingly on the Answer Sheet.
S1: One of the many young scientists who chose to throw in their lot with Rutherford was an Oxford physical chemist, Frederick Soddy.
S6: We now know that Gamma rays are a particularly fierce form of X-rays.
P: His association with Rutherford lasted only two years, but that was long enough to change the whole face of physics.
Q: He was just 23.
R: They found that thorium changed into a new element, thorium X, and in the process gave off what was apparently a gas and at the same time a third type of ray, which they named after the Greek letter 'Gamma'.
S: When he teamed up with Rutherford, they investigated thorium which, as Marie Curie had shown, was radioactive.
The proper sequence should be
View Solution
Knowledge Check
In these questions, the 1st and The last sentence of the passage are numbered 1 and 6. The rest of the passage is split into four parts and named P, Q, R and S. These four parts are not given in their proper order. Read the sentences and find out which of the four combinations is correct.
1. The fox and the crane remained friends for a long time.
P. She served the dishes in a bea ker to the fox. The fox could not eat it because the beaker was very high.
Q. The crane could not eat the dishes because of its long beak. The next day it was the turn of the crane to host thc lunch for the fox.
R. But the fox wanted to show that he was cleverer than the crane.
S. So one day he invited the crane for dinner and served the dishes on a plate. 6. The fox put down its head in shame and went away.APQRSBQSRPCRSQPDPSQR(a.) Small , circular non - history DNA also present in mitochondria and chloroplast.
(b.) The extension of plasma membranes mesosomes into, the cell can be present in the form of tubules , lamellae and vesicles.
(c.) The quasi fluid natural of lipid enables flip flop movement of proteins at a specific place.
(d.) Components of the endomembrane system associated with secretion , packaging of material and capable of digestion of several macro organic compounds.
(e.) Palade particles forming a peptide bond between amino acids is a membrane - bounded organelle.Aa and cBb and dCb,c , d and eDc and eAfter the faliure of Bohr atomic theory but its ability to explain to the atomic spectral a need was felt for the new model that could incorporate, the concept of stationary orbit, de Broglie concept, Heisenberg uncertainity principle. The concept that in corporate above facts is called quantum mechanics of the atomic model wave mchanical model. it includes set of quantum number and ∣∣ψ2∣∣ a mathematical expression of the probability of finding an electron at all points in space. This probability function is the best indication available of how the electon behaves, for as a consequence of the Uncertainity Principle, the amount we can know about the electron is limited. While quantum mechanics can tell us the exact probability of finding an electron at any two particular points, it does not tell us how the electron moves from one of these points to the other. Thus the idea of an electron orbit is lost, it is replaced with a description of where the electron is most likely to be found. This total picture of the probability of finding an electron at various points in space is called an orbital.
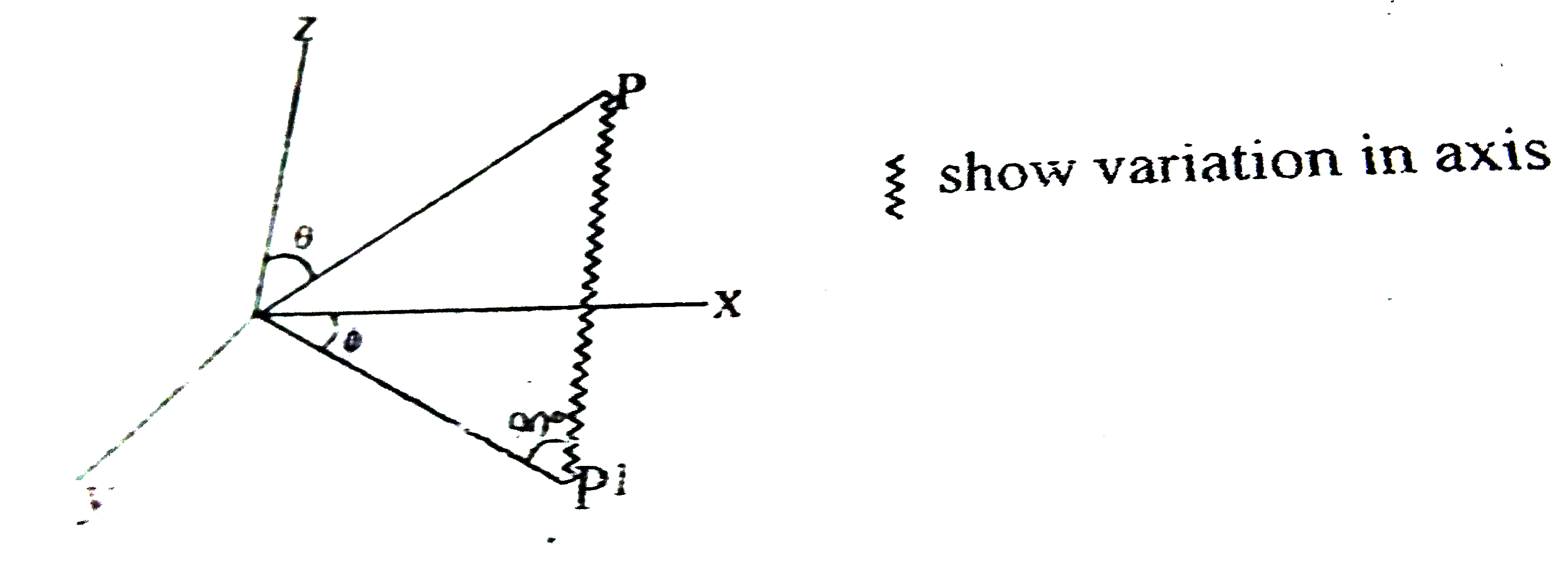
There are various types of orbitals possible, each corresponding to one of the possible combinations of quantum numbers. These orbitals are classified according to the value of n and l associated with them. In order to avoid confusion over the use of two numbers, the numerical velues of l are replaced by letters, electrons in orbitals with l=0 are called s-electrons those occupying orbitals for which l=1 are p-electrons and those for which l=2 are called d-electrons. The numerical and alphabetical correspondences are summarized in table. Using the alphabetical notation for l, we would say that in the ground state of hydrogen atom (n=1,l=0) we have a 1s-electron, or that the electron moves in a 1s-orbital. The relation of the spherical polar co-ordinates r,θ and ϕ to Cartesian coordinates x, y and z. To make the concept of an orbital more meaningful, it is helpful to examine the actual solution of the wave function for the one-electron atom. Because of the spherical sysmmetry of the atom, the wave functions are most simply expressed in terms of a spherical polar-coordinate system, shown in fig., which has its orbit at the nucleus. It is found that the wave function can be expressed as the product of two functions, one of which (the ''angular part'' X) depends only the angle θ and ϕ the other of which (the ''radial part'' R) depends only on the distance from the nucleus. Thus we have
ϕ(r,θ,ϕ)=R(r)X(θ,ϕ)
Angular and radial parts of hydrogen atom wave function
(Angular partX(θ,ϕ),,Radial partRn,l(r)),(X(s)=(14π)1/2,,R(1s)=2(za0)3/2e−σ/2),(X(px)=(34π)1/2sinθcosϕ,,R(2s)=12√2(za0)3/2(2−σ)e−σ/2),(X(py)=(34π)1/2sinθsinϕ,,R(2p)=12√6(za0)3/2σe−σ/2),(X(pz)=(34π)1/2cosθ,,),(X(d22)=(516π)1/2(3cos2θ−1),,),(X(dxz)=(154π)1/2sinθcosθcosϕ,,R(3s)=19√3(za0)3/2(6−6σ+σ2)e−σ/2),(X(dyz)=(154π)1/2sinθcosθsinϕ,,R(3p)=19√6(za0)3/2(4−σ)σe−σ/2),(X(dx2−y2)=(154π)1/2sin2θcos2ϕ,,R(3d)=19√30(za0)3/2σ2e−σ/2),(X(dxy)=(154π)1/2sin2θsin2ϕ,,),(,,σ=2Zrna0,a0=h24π2me2)
This factrorization helps us to visualize the wave function, since it allows us to consider the angular and radial dependences separately. It contains the expression for the angular and radial parts of the one electron atom wave function. Note that the angular part of the wave function for an s-orbital it alwats the same, (1/4π)1/2 regardless of principal quantum number. It is also true that the angular dependence of the p-orbitals and of the d-orbitals is independent of principle quantum number. Thus all orbitals of given types (s, p, or d) have the same angular behavour The table shows, however, that the radial part of the wave function depends both on the principal quantum n and on the angular momentum quantum number l.
To find the wave function for a particular state, we simply multiply the appropriate angular and radial parts togather called normalized wave function.
The probability of finding an electron at a point within an atom is proportional to the square of orbital wave function, i.e., ψ2 at that point. Thus, ψ2 is known as probability density and always a positive quantity.
ψ2dV(orψ2.4πr2dr). represents the probability for finding electron in a small volume dV surrounding the nucleus.
The angular wave function of which orbital with not disturb by the variation with azimuthal angle onlyA1s and 2sB2pz and 2d2zC2px and 3d2zD2px and 2s
After the faliure of Bohr atomic theory but its ability to explain to the atomic spectral a need was felt for the new model that could incorporate, the concept of stationary orbit, de Broglie concept, Heisenberg uncertainity principle. The concept that in corporate above facts is called quantum mechanics of the atomic model wave mchanical model. it includes set of quantum number and ∣∣ψ2∣∣ a mathematical expression of the probability of finding an electron at all points in space. This probability function is the best indication available of how the electon behaves, for as a consequence of the Uncertainity Principle, the amount we can know about the electron is limited. While quantum mechanics can tell us the exact probability of finding an electron at any two particular points, it does not tell us how the electron moves from one of these points to the other. Thus the idea of an electron orbit is lost, it is replaced with a description of where the electron is most likely to be found. This total picture of the probability of finding an electron at various points in space is called an orbital.
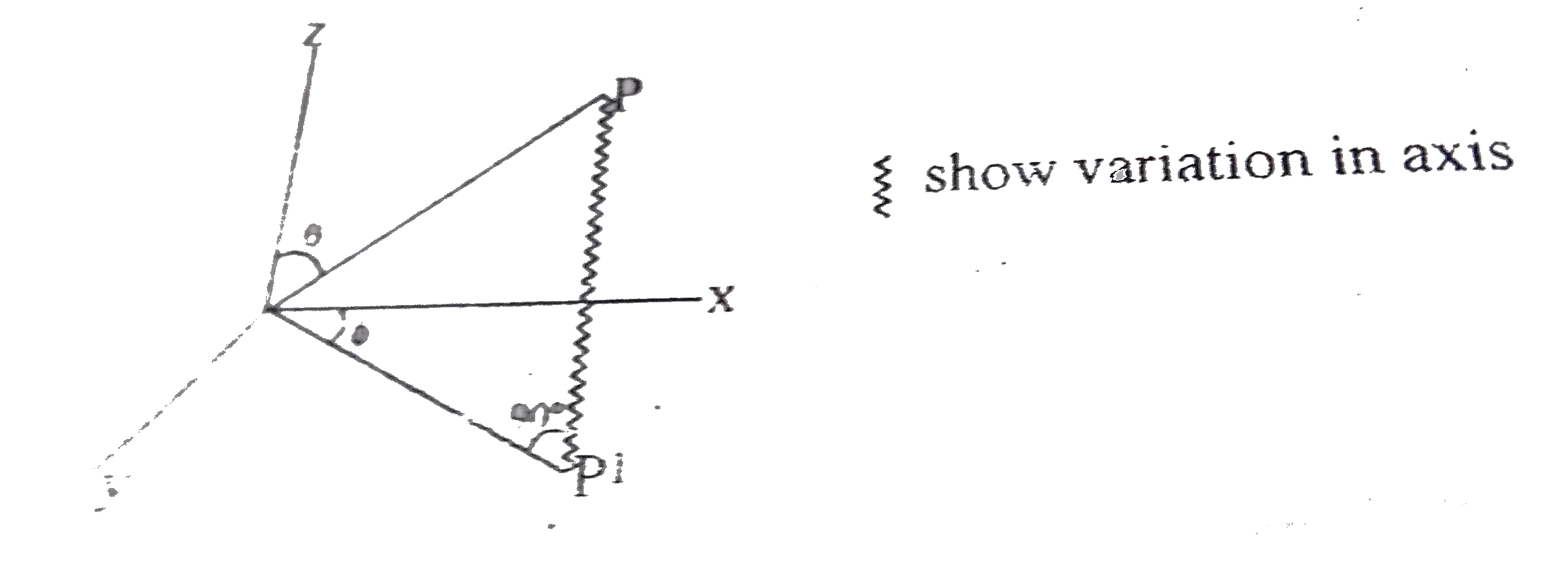
There are various types of orbitals possible, each corresponding to one of the possible combinations of quantum numbers. These orbitals are classified according to the value of n and l associated with them. In order to avoid confusion over the use of two numbers, the numerical velues of l are replaced by letters, electrons in orbitals with l=0 are called s-electrons those occupying orbitals for which l=1 are p-electrons and those for which l=2 are called d-electrons. The numerical and alphabetical correspondences are summarized in table. Using the alphabetical notation for l, we would say that in the ground state of hydrogen atom (n=1,l=0) we have a 1s-electron, or that the electron moves in a 1s-orbital. The relation of the spherical polar co-ordinates r,θ and ϕ to Cartesian coordinates x, y and z. To make the concept of an orbital more meaningful, it is helpful to examine the actual solution of the wave function for the one-electron atom. Because of the spherical sysmmetry of the atom, the wave functions are most simply expressed in terms of a spherical polar-coordinate system, shown in fig., which has its orbit at the nucleus. It is found that the wave function can be expressed as the product of two functions, one of which (the ''angular part'' X) depends only the angle θ and ϕ the other of which (the ''radial part'' R) depends only on the distance from the nucleus. Thus we have
ϕ(r,θ,ϕ)=R(r)X(θ,ϕ)
Angular and radial parts of hydrogen atom wave function
(Angular partX(θ,ϕ),,Radial partRn,l(r)),(X(s)=(14π)1/2,,R(1s)=2(za0)3/2e−σ/2),(X(px)=(34π)1/2sinθcosϕ,,R(2s)=12√2(za0)3/2(2−σ)e−σ/2),(X(py)=(34π)1/2sinθsinϕ,,R(2p)=12√6(za0)3/2σe−σ/2),(X(pz)=(34π)1/2cosθ,,),(X(d22)=(516π)1/2(3cos2θ−1),,),(X(dxz)=(154π)1/2sinθcosθcosϕ,,R(3s)=19√3(za0)3/2(6−6σ+σ2)e−σ/2),(X(dyz)=(154π)1/2sinθcosθsinϕ,,R(3p)=19√6(za0)3/2(4−σ)σe−σ/2),(X(dx2−y2)=(154π)1/2sin2θcos2ϕ,,R(3d)=19√30(za0)3/2σ2e−σ/2),(X(dxy)=(154π)1/2sin2θsin2ϕ,,),(,,σ=2Zrna0,a0=h24π2me2)
This factrorization helps us to visualize the wave function, since it allows us to consider the angular and radial dependences separately. It contains the expression for the angular and radial parts of the one electron atom wave function. Note that the angular part of the wave function for an s-orbital it alwats the same, (1/4π)1/2 regardless of principal quantum number. It is also true that the angular dependence of the p-orbitals and of the d-orbitals is independent of principle quantum number. Thus all orbitals of given types (s, p, or d) have the same angular behavour The table shows, however, that the radial part of the wave function depends both on the principal quantum n and on the angular momentum quantum number l.
To find the wave function for a particular state, we simply multiply the appropriate angular and radial parts togather called normalized wave function.
The probability of finding an electron at a point within an atom is proportional to the square of orbital wave function, i.e., ψ2 at that point. Thus, ψ2 is known as probability density and always a positive quantity.
ψ2dV(orψ2.4πr2dr). represents the probability for finding electron in a small volume dV surrounding the nucleus.
The electron probility density for 1s-orbital best represented by the relation.
View SolutionAn electromagnetic wave can be represented by E=Asin(kx−ωt+ϕ), where E is electric field associated with wave, According this equation, for any value of x,E remains sinusoidal for −∞<t<∞. Obviously this corresponds to an idealised situation because radiation from ordinary sources consists of finite size wavetrains. In general, electric field remains sinusoidal only for times of order τc' which is called coherence time. In simpler language it means that for times of order τc' a wave will have a definite phase. The finite value of coherence time could be due to many factors, for example if radiating atom undergoes collision with another atom then wave train undergoes an abrupt phase change or due to the fact that an atom responsible for emitting radiation has a finite life time in the energy level from which it drops to lower energy level, while radiating. Concept of coherence time can be easily understood using young's double slit experiment. Let interference patten is observed around point P at time t, due to superposition of waves emanting from S1 and S2 at times t=r1c and r2c respectively, where r1 and r2 are the distancesS1P&S2P. Obviously if r2−r1c<<τe,{where c=3×108m/s} then, wavetrain arriving at point P from S1 & S2 will have a definite phase relationship and an interference pattern of good contranst will be obtained.
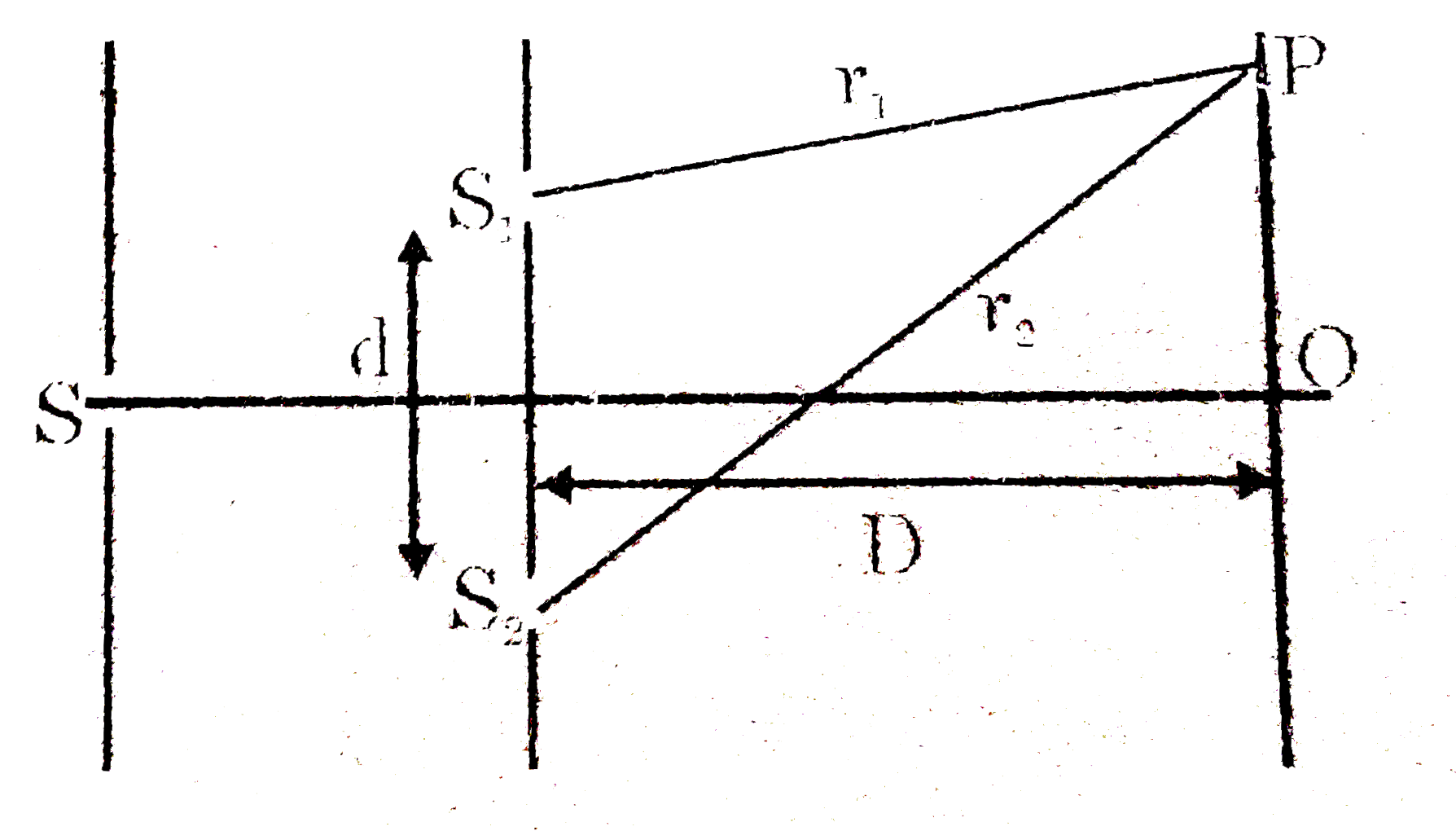
If coherence time is of order 10−10 second and screen is placed at a very large distance from slits in the given figure, then:-
View SolutionSRINIVASA RAMANUJAN (1887–1920)
Ramanujan was born on December 2, 1887, in Erode (South India) as the eldest son in a family of six children. In November 1892, he entered, the Town High School at Kumbakonam as a half-fee scholarship-holder and passed the Matriculation Examination in 1904. In the school, he became a minor celebrity, walking off with merit certificates and prizes for academic brilliance. This school nourished him for six years, bringing him as close as he would ever come to a satisfying academic experience. When he was in the seventh standard, he gave clear evidence-of his mathematical gifts, he could reel off the square root of a natural number to the specified number of places, he could point to the indeterminate nature of zero divided by zero. Ramanujan’s mother—the family being close to penuryook in college students as boarders who noticing amanujan’s interest in mathematics, brought him textbooks om the college library. Loney’s ‘Trigonometry’ was one such treasure which he mastered.
During 1906-1912, Ramanujan was constantly in search of an employer to earn his livelihood. With his “Notebooks” as his only recommendation, he sought the patronage of V. Ramaswamy Iyer, the founder of Indian Mathematical Society who was at Tirukovillur and asked for a clerical job in his office. The former had no mind to smother Ramanujan’s genius and sent him back to Madras with a letter of introduction to P.V. Seshu Aiyar, then at the Presidency College, Madras. He gave in turn, Ramanujan a letter of recommendation to that true lover of mathematics, R. Ramachandra Rao, the District Collector, Nellore. This was the turning point in his life.
On the advice of P.V. Seshu Aiyar, Ramanujan communicated his theorems on divergent series in a historic letter dated January 16, 1913 to G.H. Hardy, who was ten years senior to Ramanujan. With the personal interest of Gilbert Walker and support given by Indian stalwarts, the University of Madras awarded its first scholarship to Ramanujan to study in Cambridge. Over the next three months, Ramanujan received four long letters from Hardy, who had already sprung into action, advising the India Office, of his wish to bring him to Cambridge.
Q7. Ramanujan’s mother took in college students as boarders because
View SolutionSRINIVASA RAMANUJAN (1887–1920)
Ramanujan was born on December 2, 1887, in Erode (South India) as the eldest son in a family of six children. In November 1892, he entered, the Town High School at Kumbakonam as a half-fee scholarship-holder and passed the Matriculation Examination in 1904. In the school, he became a minor celebrity, walking off with merit certificates and prizes for academic brilliance. This school nourished him for six years, bringing him as close as he would ever come to a satisfying academic experience. When he was in the seventh standard, he gave clear evidence-of his mathematical gifts, he could reel off the square root of a natural number to the specified number of places, he could point to the indeterminate nature of zero divided by zero. Ramanujan’s mother—the family being close to penuryook in college students as boarders who noticing amanujan’s interest in mathematics, brought him textbooks om the college library. Loney’s ‘Trigonometry’ was one such treasure which he mastered.
During 1906-1912, Ramanujan was constantly in search of an employer to earn his livelihood. With his “Notebooks” as his only recommendation, he sought the patronage of V. Ramaswamy Iyer, the founder of Indian Mathematical Society who was at Tirukovillur and asked for a clerical job in his office. The former had no mind to smother Ramanujan’s genius and sent him back to Madras with a letter of introduction to P.V. Seshu Aiyar, then at the Presidency College, Madras. He gave in turn, Ramanujan a letter of recommendation to that true lover of mathematics, R. Ramachandra Rao, the District Collector, Nellore. This was the turning point in his life.
On the advice of P.V. Seshu Aiyar, Ramanujan communicated his theorems on divergent series in a historic letter dated January 16, 1913 to G.H. Hardy, who was ten years senior to Ramanujan. With the personal interest of Gilbert Walker and support given by Indian stalwarts, the University of Madras awarded its first scholarship to Ramanujan to study in Cambridge. Over the next three months, Ramanujan received four long letters from Hardy, who had already sprung into action, advising the India Office, of his wish to bring him to Cambridge.
Q8. The turning point in Ramanujan’s life came when
View SolutionSRINIVASA RAMANUJAN (1887–1920)
Ramanujan was born on December 2, 1887, in Erode (South India) as the eldest son in a family of six children. In November 1892, he entered, the Town High School at Kumbakonam as a half-fee scholarship-holder and passed the Matriculation Examination in 1904. In the school, he became a minor celebrity, walking off with merit certificates and prizes for academic brilliance. This school nourished him for six years, bringing him as close as he would ever come to a satisfying academic experience. When he was in the seventh standard, he gave clear evidence-of his mathematical gifts, he could reel off the square root of a natural number to the specified number of places, he could point to the indeterminate nature of zero divided by zero. Ramanujan’s mother—the family being close to penuryook in college students as boarders who noticing amanujan’s interest in mathematics, brought him textbooks om the college library. Loney’s ‘Trigonometry’ was one such treasure which he mastered.
During 1906-1912, Ramanujan was constantly in search of an employer to earn his livelihood. With his “Notebooks” as his only recommendation, he sought the patronage of V. Ramaswamy Iyer, the founder of Indian Mathematical Society who was at Tirukovillur and asked for a clerical job in his office. The former had no mind to smother Ramanujan’s genius and sent him back to Madras with a letter of introduction to P.V. Seshu Aiyar, then at the Presidency College, Madras. He gave in turn, Ramanujan a letter of recommendation to that true lover of mathematics, R. Ramachandra Rao, the District Collector, Nellore. This was the turning point in his life.
On the advice of P.V. Seshu Aiyar, Ramanujan communicated his theorems on divergent series in a historic letter dated January 16, 1913 to G.H. Hardy, who was ten years senior to Ramanujan. With the personal interest of Gilbert Walker and support given by Indian stalwarts, the University of Madras awarded its first scholarship to Ramanujan to study in Cambridge. Over the next three months, Ramanujan received four long letters from Hardy, who had already sprung into action, advising the India Office, of his wish to bring him to Cambridge.
Q10. Identify the correct statement:
View Solution
