Question

An ellips inscribed in a semi-cicle touches the cicular are at two distinct points and also touches the bounding diameter. Its major axis is parallel to the bounding diameter. When the ellipse has the maximum passible area, its eccentricity is -

Options

A. `(1)/(sqrt(2))`
B. `(1)/(2)`
C. `(1)/(sqrt(3))`
D. `sqrt(2/(3)`

Answer

D

Explanation

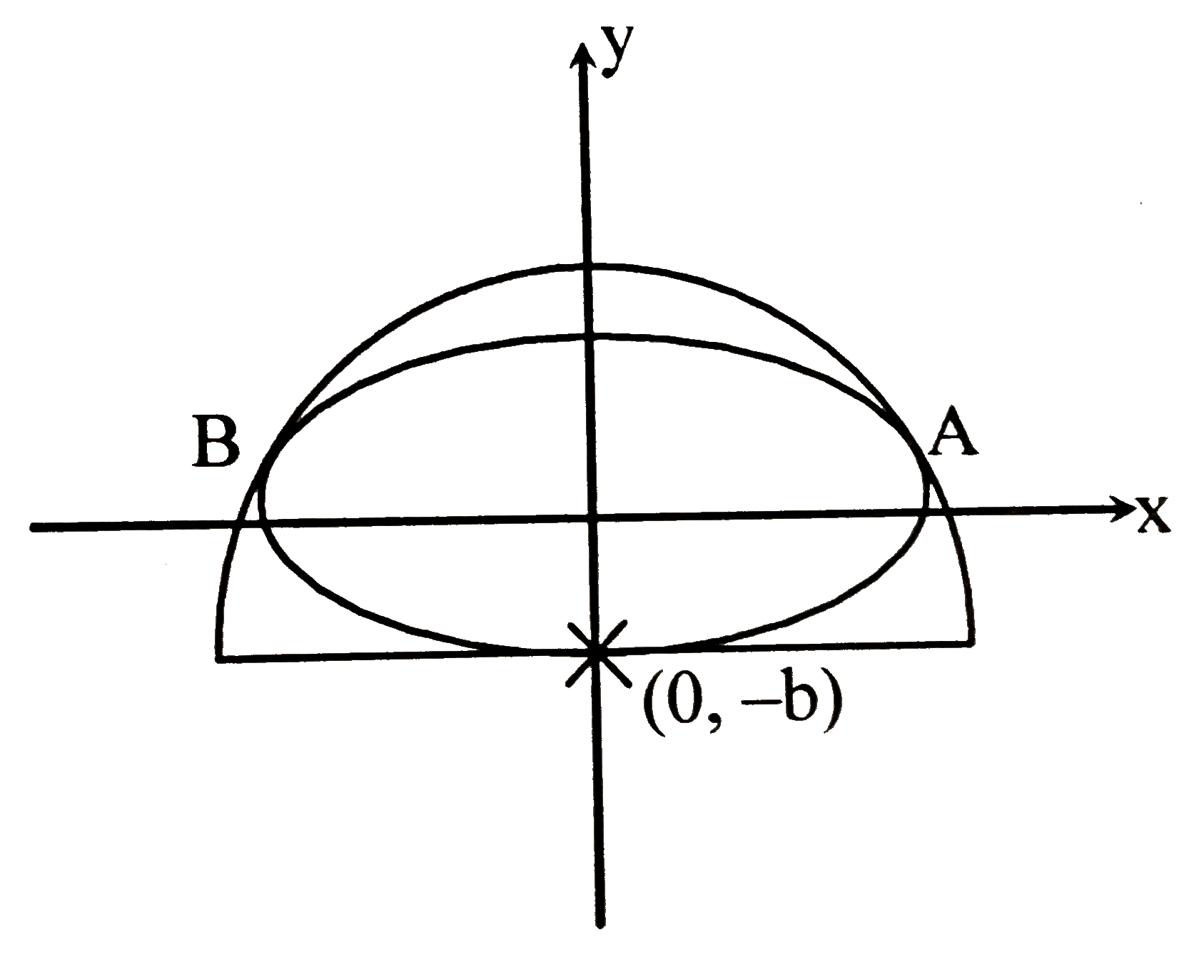
Let ellipse `(x^(2))/(a^(2))+(y^(2))/(b^(2))=1`
and circle `x^(2)+(y+b)^(2)=r^(2)" "` { let radius=2}
put ` x^(2)-a^(2)-(a^(2)y^(2))/(b^(2))`
in circle `a^()-(a^(2)y^(2))/(b^(2))+(y+b)^(2)=r^(2)`
`rArr(1-(a^(2))/(b^(2)))y^(2)+2by+(a^(2)+b^(2)-r^(2))=0`
`D=0rArrr^(2)=(a^(2))/(a^(2)-b^(2))`
`rArrb=asqrt(1-(a^(2))/(r^(2)))`
Area `=Delta=piab=pia^(2)sqrt(1-(a^(2))/(r^(2)))`
`(dDelta)/(da)=0rArra^(2)=(2r^(2))/(3)rArra=sqrt((2)/(3))r`
`:. b=asqrt(1-(2)/(3))=(a)/(sqrt(3))rArre=sqrt(2/(3))`