Let BC be a fixed line segment in the plane . The locus of a point A such that the triangle ABC is isosceles , is (with finitely many possible exceptional points )
A
a line
B
a circle
C
the union of a circle and a line
D
the union of two circles and a line
Video Solution
Text Solution
The correct Answer is:D
Case (i) :
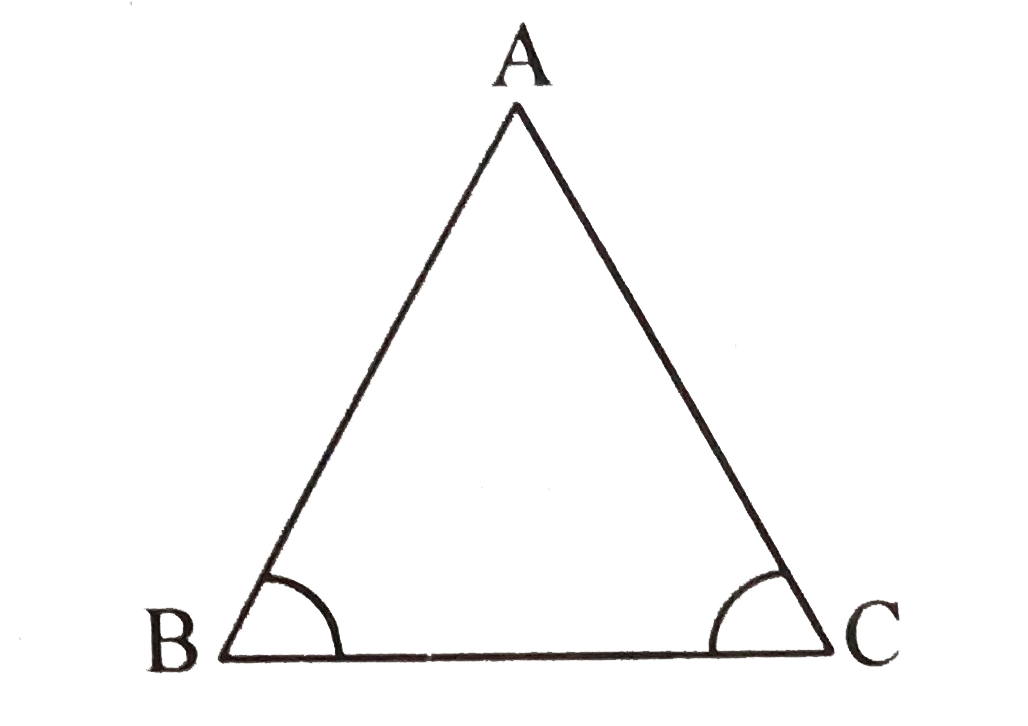
If ∠B=∠C
locus of A is ⊥ bisector of BC
So it is straight line
Case (ii) :
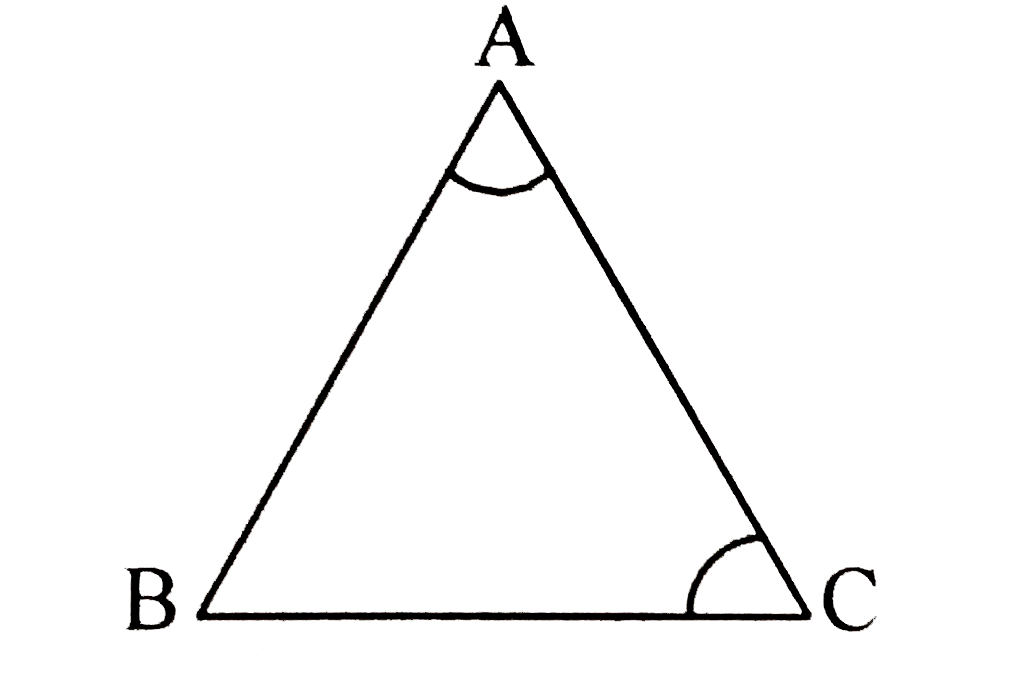
If ∠A=∠C
BC fixed B (a , 0 ) , C(0, a)
BC = AB
So , (x−a)2+y2=2a2
Circle
Case (iii) :
∠A=∠B
AC = BC
√h2+(k−a)2=√2a2
x2+(y−a)2=2a2
also a circle
So union of two circle and a line .
|
Topper's Solved these Questions
- KVPYBook:KVPY PREVIOUS YEARChapter:KVPYExercise:Part B- Mathematics
Explore 10 Videos
- KVPYBook:KVPY PREVIOUS YEARChapter:KVPYExercise:PART-1 MATHEMATICS
Explore 20 Videos
- KVPYBook:KVPY PREVIOUS YEARChapter:KVPYExercise:PART-II MATHEMATICS
Explore 10 Videos
- KVPY 2021Book:KVPY PREVIOUS YEARChapter:KVPY 2021Exercise:PART II MATHEMATICS
Explore 4 Videos
Similar Questions
Knowledge Check
Let A=(4,0),B=(0,12) be two points in the plane. The locus of a point C such that the area of triangle ABC is 18 sq. units is -
A(y+3x+12)2=81B(y+3x+81)2=12C(y+3x−12)2=81D(y+3x−81)2=12Suppose BC is a given line segment in the plane and T is a scalene triangle. The number of points A in the plane such that the triangle with vertices A,B,C (in some order) is similar to triangle T is
A4B6C12D24Let ABC be a triangle having its centroid at G. If S is any point in the plane of the triangle then SA + SB + SC is equal to
ASGB2SGC3SGD0
In triangle ABC, base BC is fixed. Then prove that the locus of vertex A such that tan B+tan C= Constant is parabola.
View SolutionLet AB be a line segment such that a point P
on the locus satisfies AB2−AP2−BP2=0 .
What is the locus ?
View SolutionLet ABC be an equilateral triangle. If the side BC is produced to the point D so that BC = 2CD, then AD2 is equal to
View SolutionIf ABC is an equilateral triangle and D is a point on BC such that AD⊥BC, then
View SolutionIf D is a Point on the side BC of a ΔABC such that AD bisects ∠BAC. Then
View Solution

