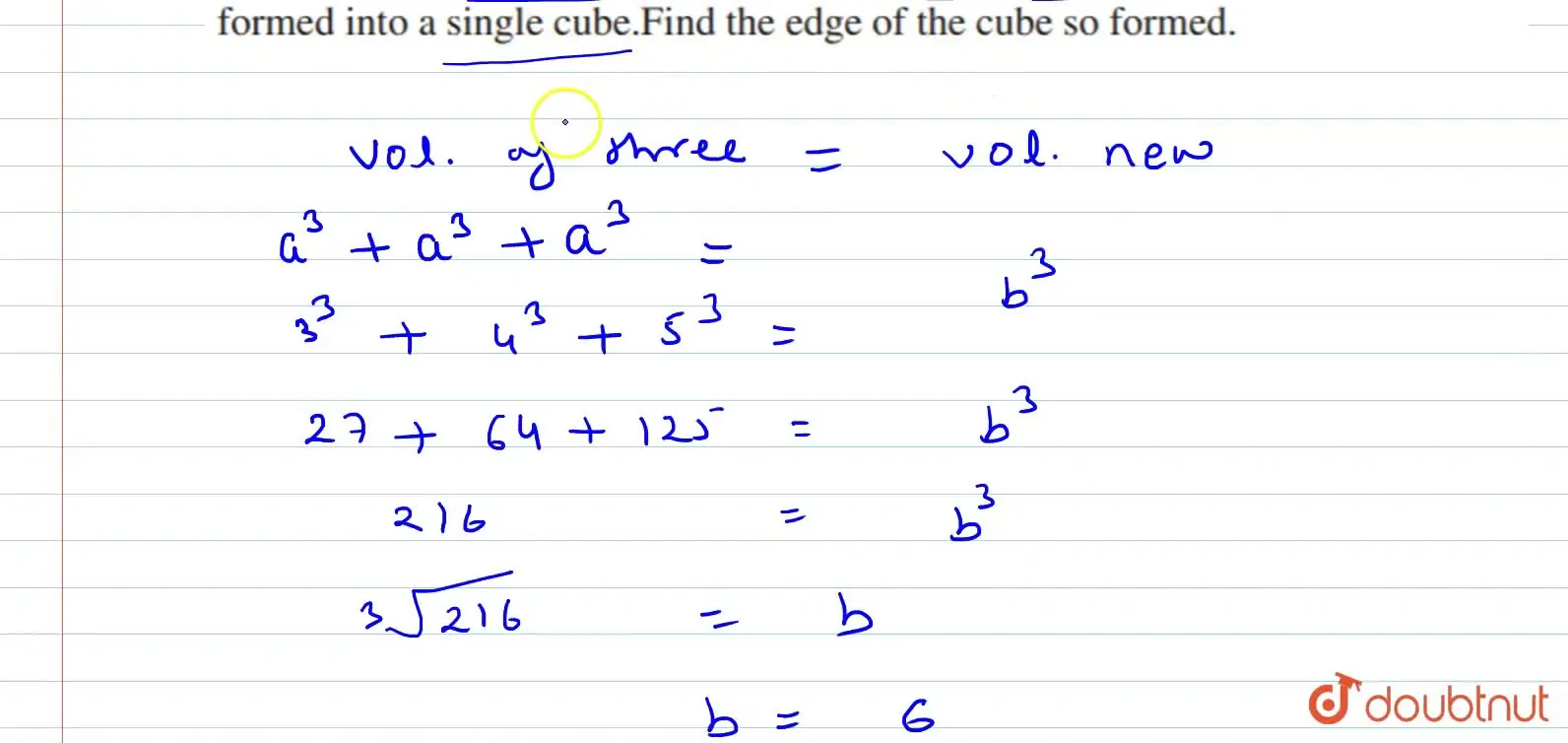Three metallic solid cubes whose edges are 3 cm ,4 cm and 5 cm melted and formed into a single cube . Find the edge of the cube formed.
Given, edges of three solid cubes are 3 cm , 4 cm and 5 cm,respectively
∴ " " Volume of first cube =(3)3=27cm3
Volume of second cube =(4)3=64cm3
and " "volume of third cube =(5)3=125cm3
∴ Sum of volume of three cubes =(27+64+125)=216cm3
Let the edge of the resulting cube = R cm
Then, volume of the resuliting cube , R3=216⇒R=cm
Related Playlists
Similar Questions
Three metallic cubes whose edges are 3 cm, 4 cm and 5 cm, are melted and recast into a single cube. Find the edge of the new cube formed.
View SolutionThree cubes of iron whose edges are 6 cm, 8 cm and 10 cm respectively are melted and formed into a single cube. The edge of the new cube formed is
View SolutionThree cubes of iron whose edges are 6 cm, 8 cm and 10 cm respectively are melted and formed into a single cube. The edge of the new cube formed is
View SolutionThree metallic solid cubes of sides 6 cm, 8 cm and 10 cm are melted to form a single cube. The length of the edge of the new cube is
View SolutionThree cubes of iron whose edges are 6 cm, 8 cm and 10 cm respectively formed into a single cube. The edge of the new cube is
View SolutionThree metal cubes whose edges measure 3cm, 4cm and 5cm respectively are melted to form a single cube. Find its edge. Also, find the surface area of the new cube.
View SolutionThree metal cubes with edges 6cm , 8cm and 10cm respectively are melted together and formed in to a single cube. Find the diagonal of this cube.
View SolutionThree metallic solid cubes of sides 6 cm cm and 10 cm are melted to form a sin cube. The length of the edge of the n cube is :
View SolutionThree cubes of metal whose edges are 6 cm, 8 cm and 10 cm respectively are melted to form a single cube. The edge of the new cube is
View SolutionThree metal cubes of sides 5 cm, 4 cm and 3 cm respectively are melted and recast into a new cube. The edge of the new cube so formed is ____ cm.
View Solution