An ice-ceram cone full of ice-cream having radius 5 cm height 10 cm as shown if figure.
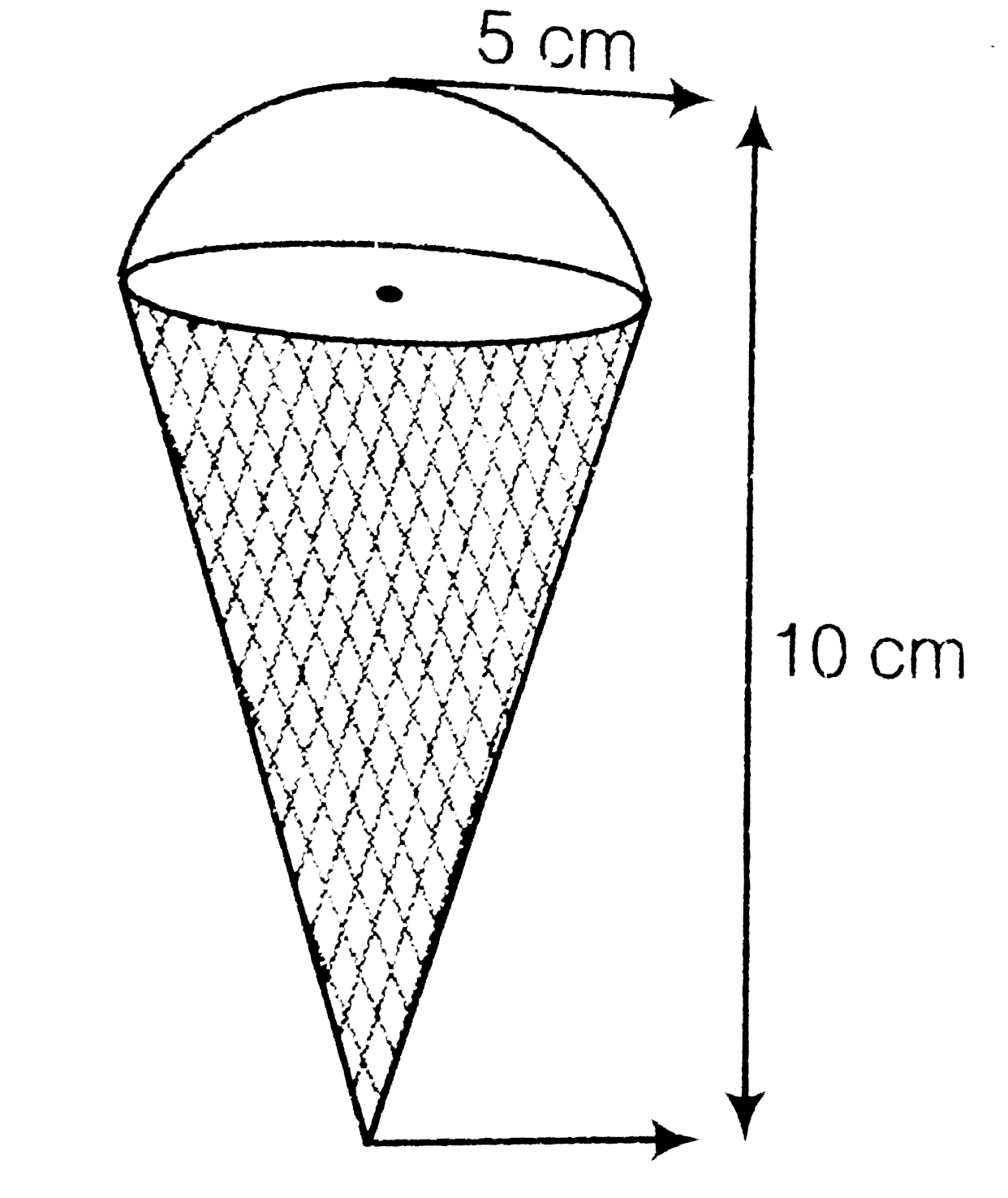
Calculate the volume of ice-cream, provided that its 16 part is left unfilled with ice-cream.
The correct Answer is:=327.4cm3
Given , ice - cream cone is the combination of a hemisphere and a cone.
Also, radius of hemisphere = 5 cm
∴ Volume of hemisphere =23πr3=23×227×(5)3
=550021=261.90cm3
Now, radius of the cone = 5 cm
and heigth of the cone = 10-5 = cm
∴ Volume of the cone =13πr2h
=13×227×(5)2×5
=275021=130.95cm3
Now, total volume of ice- cream cone=261.90+130.95=392.85cm3
Since,16 parts is left unfilled with ice- cream.
∴ Required volume of ice - cream =392.85−392.85×16=392.85−64.475
=327.4cm3
Topper's Solved these Questions
Similar Questions
Combination of sphere and cone : A right circular cylinder having diameter 12 cm and height 15 cm is full of ice-cream. The ice cream is to be filled in cones of height 12 cm and diameter 6 cm having a hemispherical shape on the top. Find the number of cones which can be filled with ice-cream.
View SolutionA container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice-cream. The ice-cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
View Solution
Knowledge Check
An ice-cream cone is an example of a
AcuboidBcubeCpyramidDnone of theseA right circular cylinder having diameter 21 cm and height 38 cm s full of ice cream. The ice cream is to be filled in cones of height 12 cm and diameter 7 cm having a hemispherical shape on the top. The number of each cones to be filled with ice cream is
A54B44C36D24
A right circular cylinder having diameter 12 cm and height 15 cm is full ice-cream. The ice-cream is to be filled in cones of height 12 cm and diameter 6 cm having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
View SolutionA cylindrical ice-cream pot of radius 6 cm and height 21 cm full of ice cream. The ice cream is to be filled in cones of height 12 cm and radius 3 cm. Ice cream on the top of the cone has hemispherical shape. How many such cones can be filled with ice cream?
View SolutionA container sphaded like a right circular cylinder having radius 6cm and height 15cm is full of ice-cream.The ice-creams is to be filled into cones of height 12 cm and diameter 6cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
View SolutionA right circular cylinder having diameter 12cm and height 15cm is full of ice-cream. The ice-cream is to be filled in cones of height 12cm and diameter 6cm having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
View SolutionA right circular cylinder having diameter 12 cm and height 15 cm is full of ice cream. The ice cream is to be filled in cones of height 12 cm and diameter 6 cm having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.
View SolutionAn ice cream cone of mass M has base radius R and height h. Assume its wall to be thin and uniform. When ice cream is filled inside it (so as to occupy the complete conical space) its mass becomes 5M. Find the distance of the centre of mass of the ice cream filled cone from its vertex.
View Solution

