A man 2m tall, walks at the rate of 123m/sec towards a street light which is 513 m above the ground. At what rate is tip of his shadow moving? At what rate is the length of the shadow changing when he is 3113m from the base of the light?
Let AB be the street light post and CD be the height of man i.e., CD = 2m.
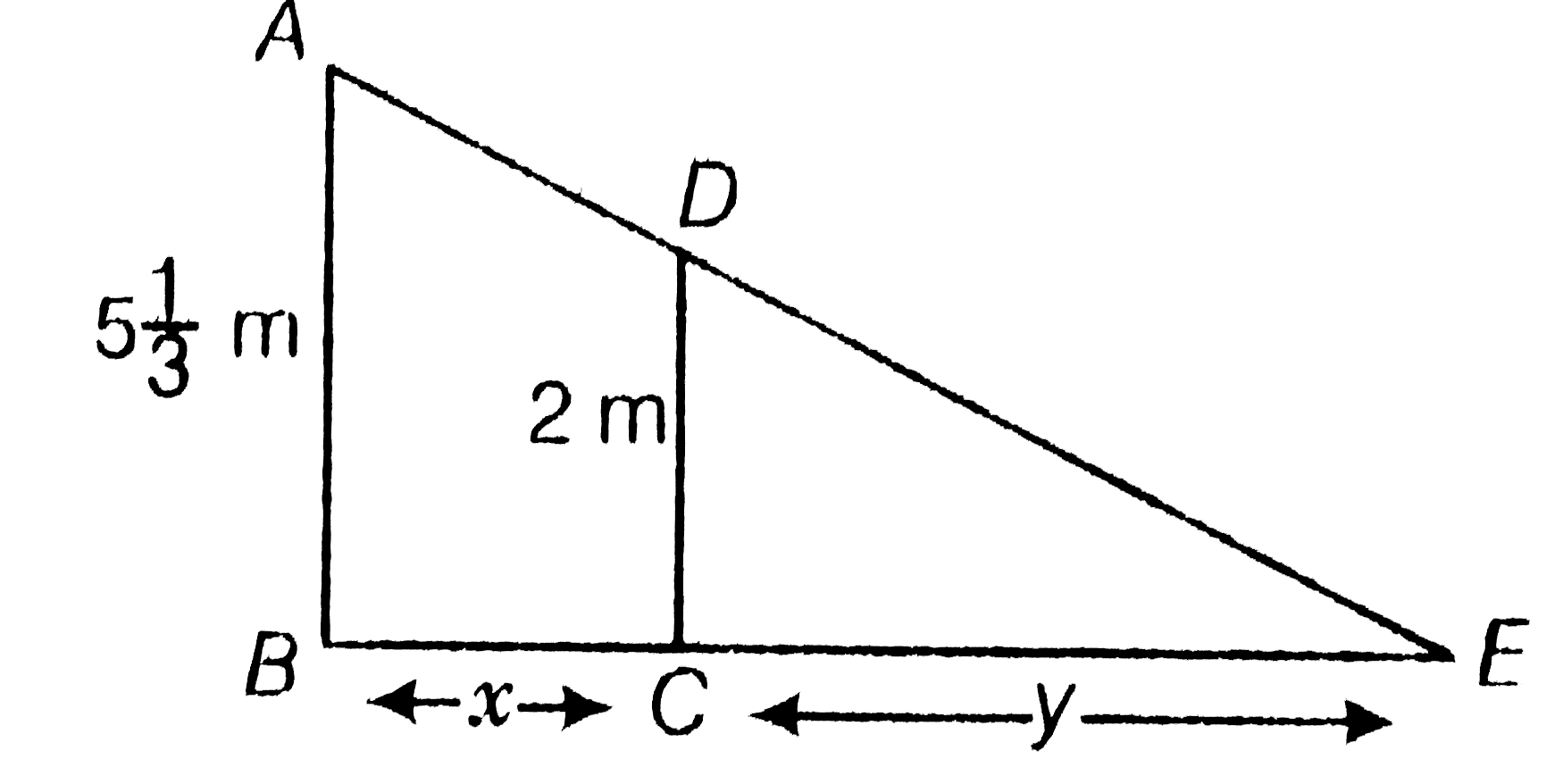
Let BC= xm, CE=ym and dxdt=−53m/s.
From ΔABE and ΔDCE, we see that
ΔABE~ΔDCE
∴ABDC=BECE⇒1632=x+yy
⇒166=x+yy
⇒16y=6x+6y⇒10y=6x
⇒y=35x
On differentiating both sides w.r.t. t, we get
dydt=35.dxdt=35.(−123)
Since, man is moving towards the light post
=35.(−53)=−1m/s.
Let z=x+y
Now, differentiating both sides w.r.t. t, we get
dzdt=dxdt+dydt=−(53+1)
=−83=−223m/s.
Hence, the tip of shadow is moving at the rate of 223m/s
Hence, the tip of shadow is moving at the rate of 223m/s towards the light source and length of the shadow is decreasing at the rate of 1m/s.
Topper's Solved these Questions
Similar Questions
A man 2m tall, walks at the rate of 123m/sec towards a street light which is 513 m above the ground. At what rate is tip of his shadow moving? At what rate is the length of the shadow changing when he is 3113m from the base of the light?
View SolutionA man 2 m tall,walks at the rate of 53ms towards a street light which is 163m above the ground.At what rate is the tip of his shadow moving? At what rate is the length of the shadow changing when he is 103m from the base of the light?
View Solution
Knowledge Check
A man of height 150 cm walks at the rate of 75cm/sec, towards a lighted lamp-post which is 450 cm high. When he is 360cm away from the lamp-post , his shadow is shortening at the rate of
A37.5cm/secB75.3cm/sec.C57.3cm/sec.D3.75cm/sec.
A man 180 cm tall walks at a rate of 2m/sec. away, from a source of light that is 9 m above the ground. How fast is the length of his shadow increasing when he is 3 m away from the base of light?
View SolutionA man 1.6 m high walks at the rate of 30 metre per minute away from a lamp which is 4m above ground . How fast does the man’s shadow lengthen ?
View SolutionA man 160 cm tall, walks away from a source of light situated at the top of a pole 6m high at the rate of 1.1 m/sec. How fast is the length of his shadow increasing when he is 1 metre away from the pole.
View SolutionA man is walking at the rate of 6.5 km/hr towards the foot of a tower 120m high. At what rate is he approaching the top of the tower when he is 5m away from the tower?
View SolutionA man who is 1.6 m tall walks away from a lamp which is 4 m above ground at the rate of 30 m/min. How fast is the man's shadow lengthening?
View SolutionA man of height 160 cm walks at a rate of 1.1 m/sec from a lamp post which 6m high. Find the rate at which the length of his shadow increases when he is 1m away from the lamp post.
View SolutionA man of height 1.7 m walks at a uniform speed of 6.6 m/min from a lamp post which is 5m high.Find the rate at which the length of his shadow increases.
View Solution

