Two mercury droplets of radii 0.1 cm and 0.2 cm collapse into one single drop. What amount of energy is released? The surface tension of mercury T=435.5×10−3Nm−1
Consider the diagram
Radii of mercury droplets r1=0.1cm=1×10−3m
r2=0.2cm=2×10−3 m
Surface tension (T) =435.5×10−3 N/m
Let the radius of the big drop formed by collapsing be R.
∴ Volume of big drop=Volume of small droplets
43πR3=43πr31+43πr22
or R3=r31+r32
=(0.1)3+(0.2)3
=0.001+0.008
=0.009
or R=0.21cm=2.1×10−3m
∴ change in surface area ΔA=4πR2−(4πr21+4πr22)
=4π[R2−(r21+r22)]
∴ Energy released =T.ΔA (where T is surface tension of mercury)
=T×4π[R2−(r21+r22)]
=435.5×10−3×4×3.14[(2.1×10−3)2−(1×10−6+4×10−6)]
=435.5×4×3.14[4.41−5]×10−6×10−3
=−32.23×10−7 (Negative sign shows absorption)
Therefore, 3.22×10−6 J energy will be absorbed.
Note In this process, energy is not conserved . Energy is 1st due to the collapsing in the form of radiations.
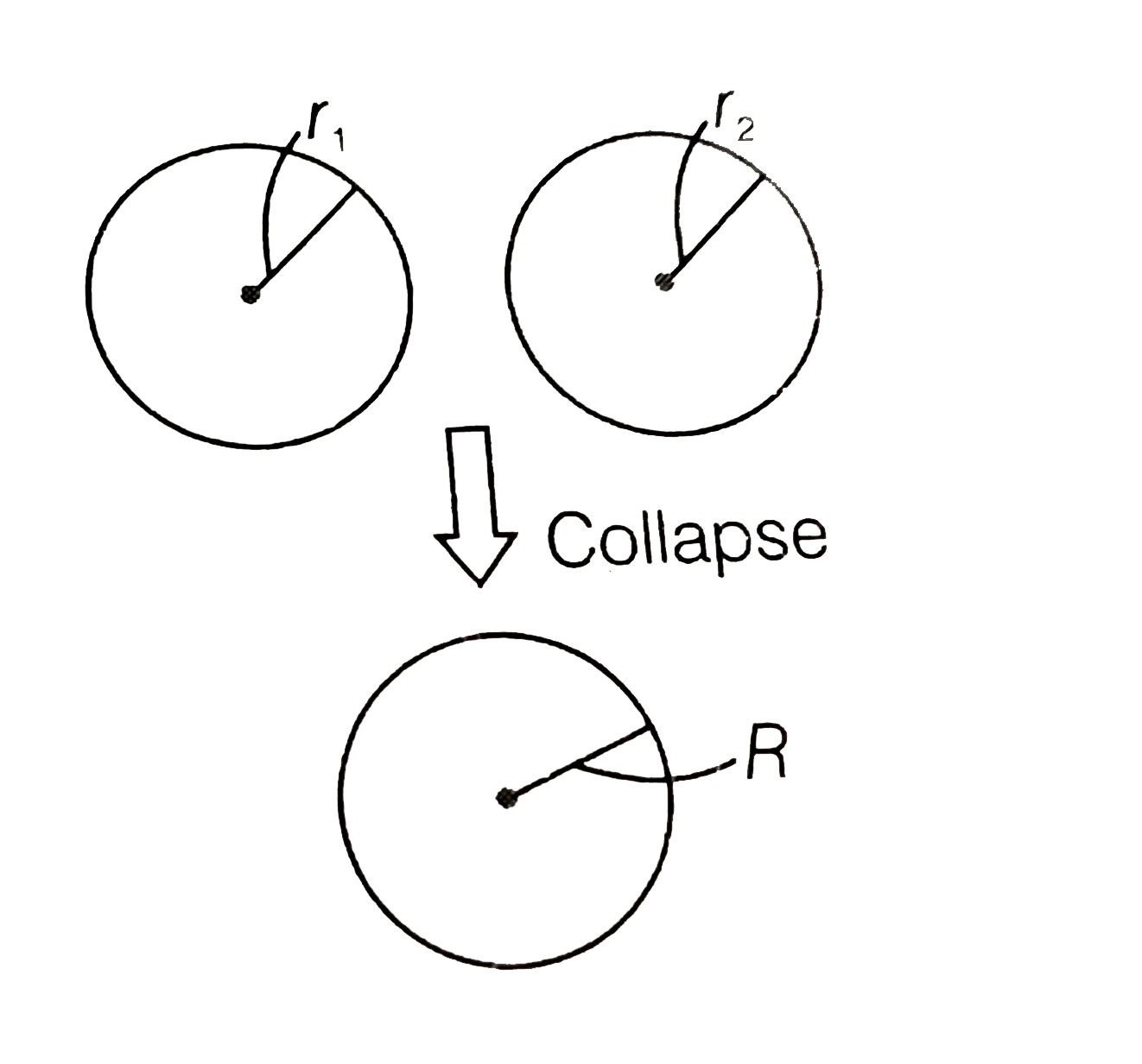
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT EXEMPLARCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Long Answer Type Questions
3 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT EXEMPLARCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Very Short Answer Type Questions
5 Videos
- LAWS OF MOTIONBOOK - NCERT EXEMPLARCHAPTER - LAWS OF MOTIONEXERCISE - Long answer Type Questions
9 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT EXEMPLARCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LONG SHORT ANSWER TYPE QUESTION
16 Videos
Similar Questions
Two mercury droplets of radii 0.2 cm and 0.4 cm collapse into one single drop. What amount of energy is released? The surface tension of mercury 440×10−3Nm−1 and g=10ms−2.
View SolutionA mercury drop of radius 1 cm is sprayed into 106 dropletes of equal size. Calculates the energy expanded if surface tension of mercury is 35×10−3N/m.
View Solution
Knowledge Check
Two mercury droplets radii 0.1 cm and 0.2 cm collapse into one single drop. What amount of energy is released/absorbed? The sur4face tension of mercury T=435.5×10−3Nm−1
A32.23×10−7 (Released)B32.23×10−7 (Absorbed)C64.46×10−7 (Absorbed)D64.46×10−7 (released)A mercury drop of radius 1.0 cm is sprayed into 106 droplets of equal sizes. The energy expended in this process is (Given, surface tension of mercury is 32×10−2Nm−1)
A3.98×10−4JB8.46×10−4JC3.98×10−2JD8.46×10−2JTwo mercury drops (each of radius r) merge to form a bigger drop. The surface energy of the bigger drop, if T is the surface tension is
A25/3πr2B4πr2TC2πr2TD28/3πr2
A menisus drop of radius 1 cm sprayed into 105 droplets of equal size . Calculate the energy expended if surface tension of mercury is 435×10−3 N/m
View SolutionA mercury drop of radius 1.0cm is sprayed into 108 droplets of equal size. Calculate the energy expanded. (Surface tension of mercury =32×10−2N/m).
View SolutionA mecury drop of radius 1 cm is sprayed into 105 droplets of equal size. Calculate the increase in surface energy if surface tension of mercury is 35×10−3N/m.
View SolutionA mercury drop of radius 1 cm is sprayed into 106 drops of equal size. The energy expended in joule is (surface tension of mercury is (460×10−3N/m)
View SolutionWhat is the excess pressure inside a drop of mercury of radius 3.0 mm? (Surface tension of mercury is 4.65×10−1Nm−1)
View Solution
