The velocity of a body of mass 2kg as a function of t is given by υ(t)=2tˆi+t2ˆj Find the momentum and force acting on it at time t=2s.
Given , mass of the body m = 2kg
Velocity of the body v(t) = 2tˆi+t2ˆj
∴ Velocity of the body at t = 2s
v=2×2ˆi+(2)2ˆj=(4ˆi+4ˆj)
Momentum of the body (p) = mv = 2(4ˆi+4ˆj)=(8ˆi+8ˆj) kg-m/s
Acceleration of the body (a) = dvdt
= ddt(2tˆi+t2ˆj)
= 2(ˆi+2tˆj)
At t = 2 s
a = (2ˆi+2×2ˆj)
= (2ˆi+4ˆj)
Force acting on the body (F) = ma
= 2(2ˆi+4ˆj)
= (4ˆi+8ˆj)N
Topper's Solved these Questions
- LAWS OF MOTIONBook:NCERT EXEMPLARChapter:LAWS OF MOTIONExercise:Short answer type questions
Explore 6 Videos
- LAWS OF MOTIONBook:NCERT EXEMPLARChapter:LAWS OF MOTIONExercise:Long answer Type Questions
Explore 9 Videos
- LAWS OF MOTIONBook:NCERT EXEMPLARChapter:LAWS OF MOTIONExercise:Mutiple Choice Questions (More than One Options)
Explore 6 Videos
- KINETIC THEORYBook:NCERT EXEMPLARChapter:KINETIC THEORYExercise:Multiple Choice Questions (MCQs)
Explore 31 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NCERT EXEMPLARChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Long Answer Type Questions
Explore 3 Videos
Similar Questions
Knowledge Check
The position (x) of a particle of mass 1 kg moving along X-axis at time t is given by (x=12t2) metre. Find the work done by force acting on it in time interval from t=0 to t=3s.
A4.2 JB5.4 JC4.6 JD4.5 JThe time dependence of the position of a particle of mass m = 2 is given by →r(t)=2tˆi−3t2ˆj Its angular momentum, with respect to the origin, at time t = 2 is :
A−34(ˆk−ˆi)B−48ˆkC36ˆkD48(ˆi+ˆj)The displacement of a body of mass 2 kg varies with time t as S=t2+2t, where S is in m and t is in s. The work done by all the forces acting on the body during the time interval t=2 to t=4 s is
A36 JB64 JC100 JD120 J
The position (x) of a particle of mass 2 kg moving along x-axis at time t is given by x=(2t3) metre. Find the work done by force acting on it in time interval t=0 to t=2 is :-
View SolutionThe mass of a body is 2.5 Kg. it is in motion and its velocity υafter time t is υ=t33+t22+1
Calculate the force acting on the body at the time t =3 s.
View SolutionThe position time graph of a body of mass 2kg is as given in What is the impulse on the body at t=0 s and t=4s ?
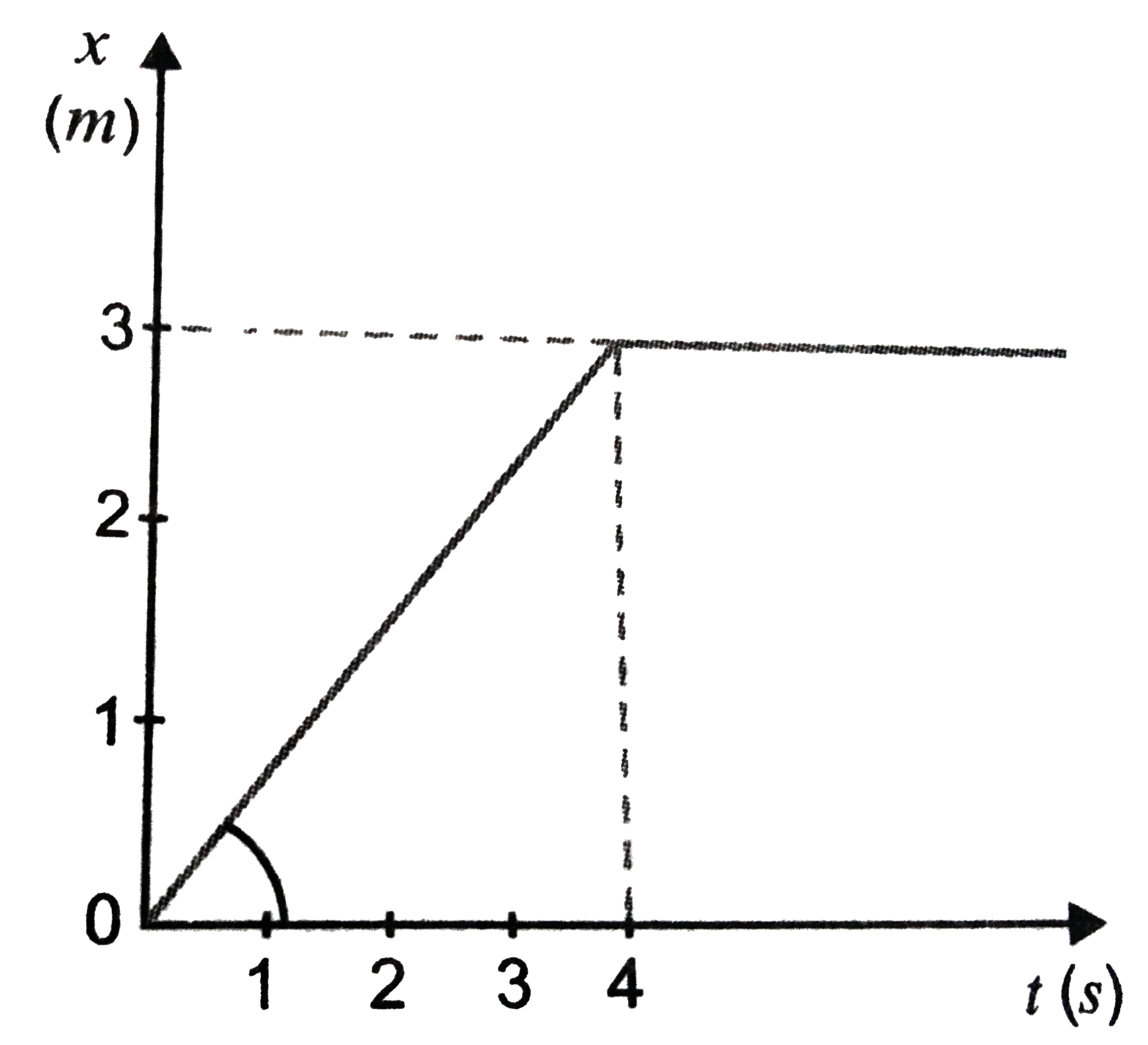 .
.
View SolutionThe velocity vector of the motion described by the position vector of a particle, r=2tˆi+t2ˆj is given by
View SolutionThe displacement of a body of mass 2kg varies with time t as S=t2+2t, where S is in seconds. The work done by all the forces acting on the body during the time interval t=2s to t=4s is
View Solution

