A body a of mass m slides on plane inclined at angle θ0 to the horizontal and μ1 is the coefficient of friction between A and the plane A is connected by a light string passing over a frictionless pulley to another body B also of mass m slidding on a frictionless plane inclined at angle θ2 to the horizontal Which of the following statements are ture ? 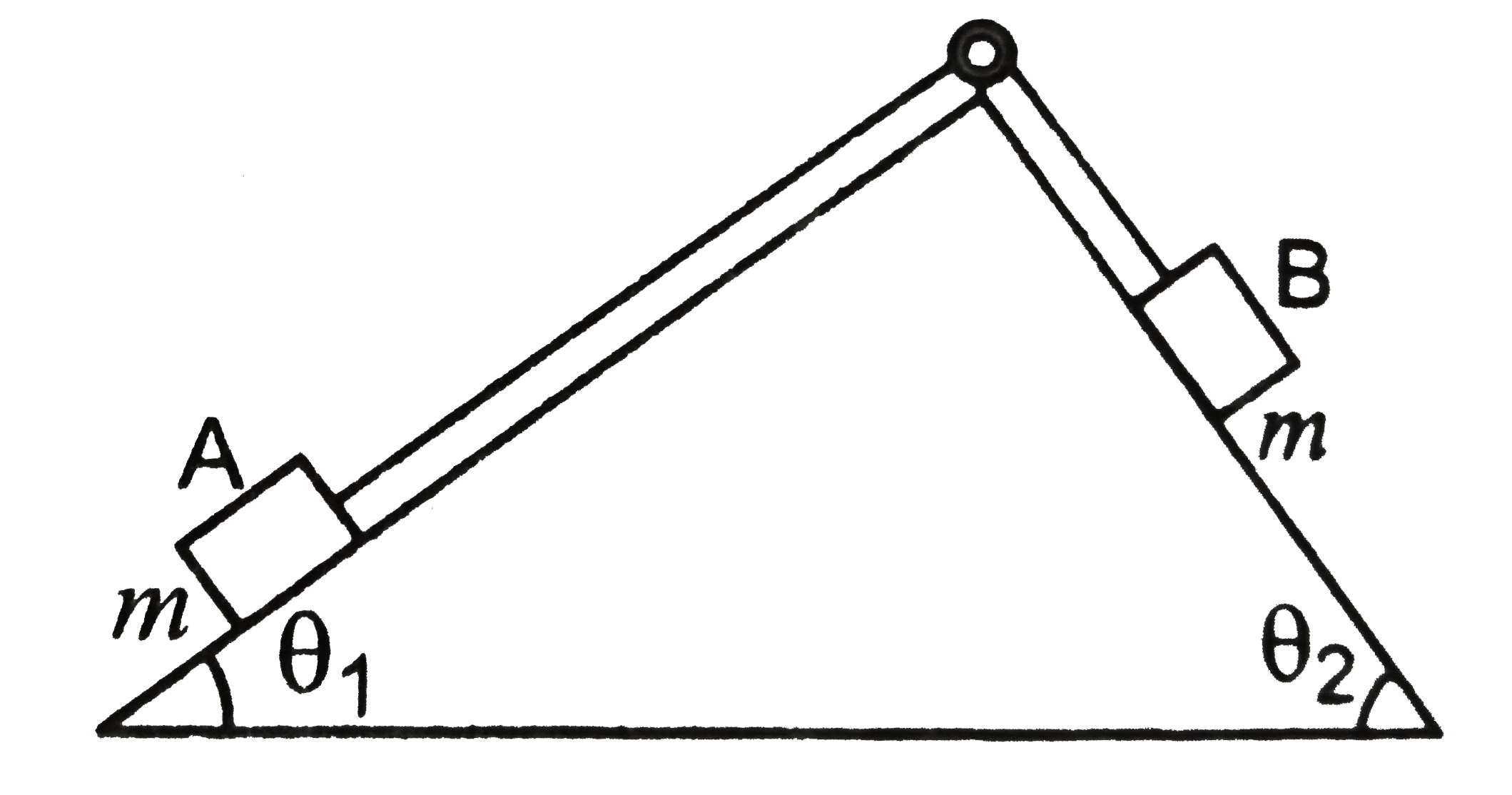 .
.
A will never move up the plane
A will just start moving up the plane when μ=sinθ2−sinθ1cosθ1
For A to move up the plane θ2 , must always be greater than θ1
B will always slide down with constant speed
The correct Answer is:B, C
Let A moves up the plane frictional force on A will be downward as shown .
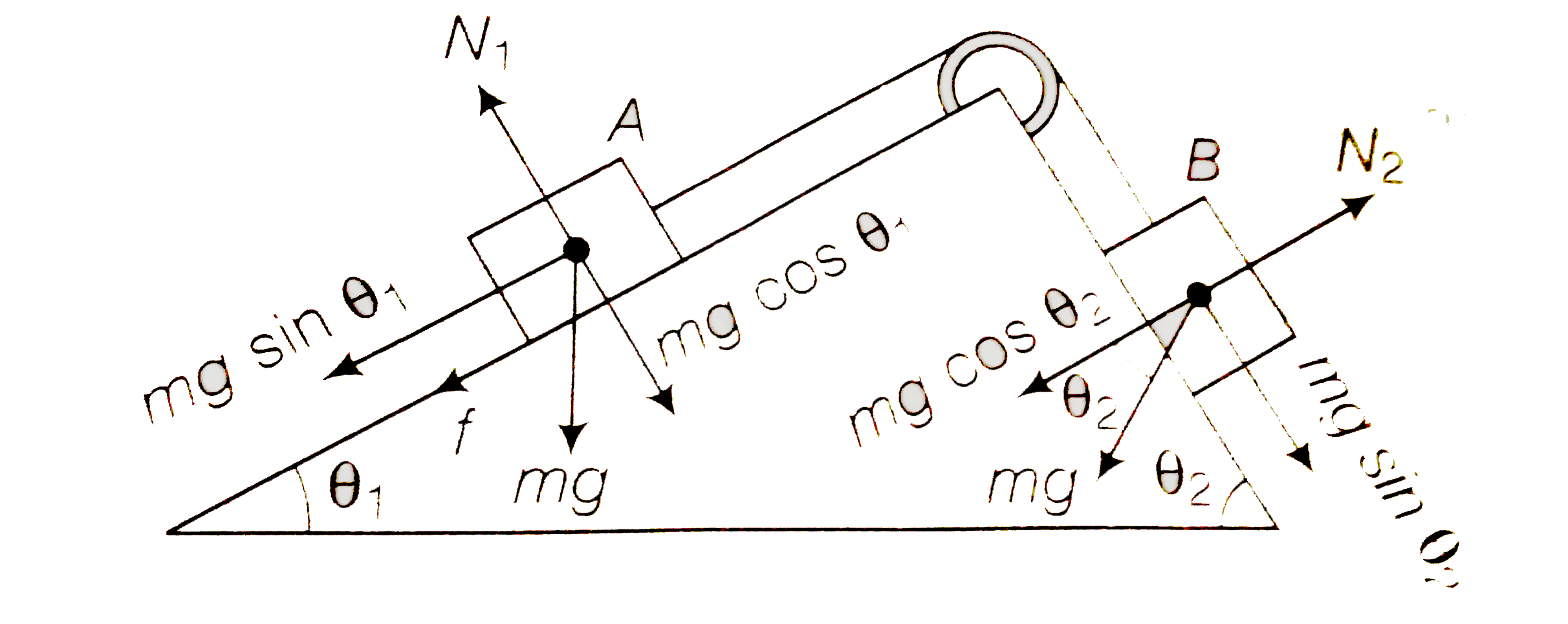
When A just starts moving up
mg sin θ1+f=mgsinθ2
⇒ mgsinθ1+μmgcosθ1=mgsinθ2
⇒ =sinθ2−sinθ1cosθ1
When A moves upwards
f = mg sin θ2−mgsinθ1>0
⇒ sinθ2>sinθ1⇒θ2>θ1
Topper's Solved these Questions
- LAWS OF MOTIONBook:NCERT EXEMPLARChapter:LAWS OF MOTIONExercise:Very short answer type Questions
Explore 12 Videos
- LAWS OF MOTIONBook:NCERT EXEMPLARChapter:LAWS OF MOTIONExercise:Short answer type questions
Explore 6 Videos
- LAWS OF MOTIONBook:NCERT EXEMPLARChapter:LAWS OF MOTIONExercise:Long answer Type Questions
Explore 9 Videos
- KINETIC THEORYBook:NCERT EXEMPLARChapter:KINETIC THEORYExercise:Multiple Choice Questions (MCQs)
Explore 31 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NCERT EXEMPLARChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Long Answer Type Questions
Explore 3 Videos
Similar Questions
A body of mass m slides down a rough plane of inclination α . If μ is the coefficient of friction, then acceleration of the body will be
View SolutionA body is sliding down an inclined plane forming an angle 30∘ with the horizontal. If the coefficient of friction is 0.3 then acceleration of the body is
View Solution
Knowledge Check
A block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
AmgcosθB√μ2+1mgcosθCμmgcosθ√μ2+1DμmgθA body of mass m slides down an inclined plane making an angle of 45∘ with the horizontal. If the coefficient of friction between the body and the plane be 0.3, the acceleration of the body is approximately equal to :
A0.22 gB0.30 gC0.49 gD0.70 gA block of mass m is placed at rest on an inclination θ to the horizontal.If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
AmgBμmgcosθCmgsinθDμmgtanθ
A body of mass m slides down a rough plane of inclination α . If μ is the coefficient of friction, then acceleration of the body will be
View SolutionA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View SolutionA body takes just twice the time as long to slide down a plane inclined at 30∘ to the horizontal as if the plane were frictionless. The coefficient of friction between the body and the plane is
View SolutionA small mass slides down an inclined plane of inclination θ the horizontal the coefficient of friction is m=μ0x, where x is the distance by the mass before it stops is .
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View Solution

