Replace A,B and C by suitable numerals. 5A+87 CB3
The correct Answer is:A=6, B=4, C=1
Step by step video, text & image solution for Replace A,B and C by suitable numerals. ({:(," "5A),(,+87):})/(" "C B3) by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Related Playlists
- BOOK - RS AGGARWALCHAPTER - PLAYING WITH NUMBERSEXERCISE - Exercise 5D9videos
PLAYING WITH NUMBERS
- BOOK - RS AGGARWALCHAPTER - PLAYING WITH NUMBERSEXERCISE - Test Paper-511videos
PLAYING WITH NUMBERS
- BOOK - RS AGGARWALCHAPTER - PLAYING WITH NUMBERSEXERCISE - Exercise 5B15videos
PLAYING WITH NUMBERS
- BOOK - RS AGGARWALCHAPTER - PIE CHARTS EXERCISE - Exercise 24B4videos
PIE CHARTS
- BOOK - RS AGGARWALCHAPTER - POLYGONSEXERCISE - EXERCISE 14B14videos
POLYGONS
Similar Questions
Replace A,B and C by suitable numerals. AB ×3 CAB
View SolutionReplace A,B and C by suitable numerals. 6A−AB 37
View SolutionReplace A,B and C by suitable numerals. CB5−28A 259
View SolutionReplace A,B and C by suitable numerals. A+A A BA
View SolutionReplace A,B and C by suitable numerals. AB×BA (B+1)CB
View SolutionReplace A,B,C by suitable numberals:
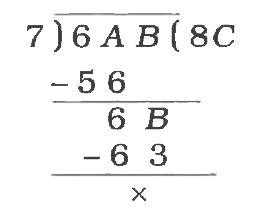 View Solution
View SolutionReplace A,B and C by suitable numerals. 4CB6+369A 8173
View SolutionReplace A,B,C by suitable numberals:
57A−CB8 293View SolutionReplace A,B,C,D by suitable numerals in the following
6AB5+D58C 9351View SolutionIf a,b,c and d satisfy the equations
a+7b+3c+5d=08a+4b+6c+2d=−42a+6b+4c+8d=45a+3b+7c+d=−4then (a+d)/(b+c)=?View Solution


