Two identical current carrying coaxial loops, carry current I in an opposite sense. A simple amperian loop passes through both of them once. Calling the loop as C,
∮B.dl=mμ0I
The value of ∮B.dl=−+2μ0I is independent of sense of C.
There may be z point of C where, B and dl are perpendicular
B vanishes everywhere on C.
The correct Answer is:B, C
Applying the ampere's circuital law, we have
∮=B.dl=μ0(I−I)=0 (because current is in opposite sence).
Also, there may be a point on C where B and dl are perpendicular and hence,
∮cB.dl=0.
Topper's Solved these Questions
Similar Questions
torque on current carrying loop
View SolutionTwo co-axial identical circular current carrying loops are shown in figure, currents in them are in the same directions. Now, match the following two columns.
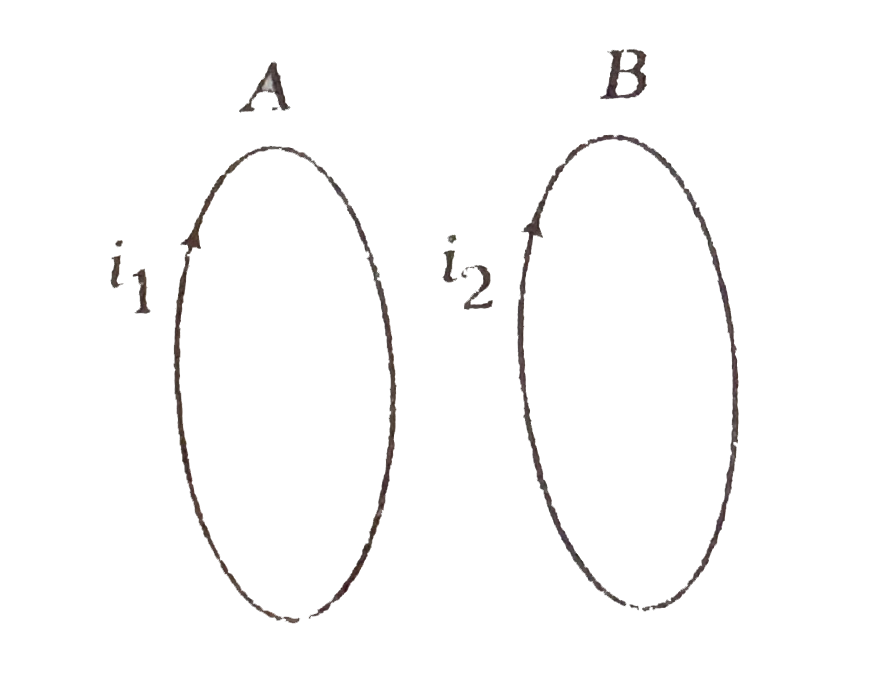
Column IColums IIA.Current i1 is increasedp.Loops will attract each otherB.Current i2 is decreasedq.Loops will repel each otherC.Loop-1 is moved towards loop-2r.Current i1 will increaseD.Loop-2 is moved away from loop-1s.Current i2 will increase
View Solution
Knowledge Check
Current carrying circular loop acts as
AMagnetic dipoleBMagnetic fluxCMagnetic fieldDCondenserTwo identical coaxial circular loops carry a current i each circulating int the same direction. If the loops approch each other the current in
Aeach decreasesBeach increasesCeach remain the sameDone increases whereas that in the other decreasesTwo circular, similar, coaxial loops carry equal currents in the same direction. If the loops are brought nearer, what will happen?
Acurrent will increase in each loopBcurrent will decrease in each loopCcurrent will remain same in each loopDcurrent will increase in one and decrease in the other
A current carrying loop in a uniform magnetic field will experience
View SolutionA current carrying loop lies on a smooth horizontal plane. Then,
View SolutionA current carrying squre loop is placed near an infinitely long current carrying wire as shown in figure . The loop torque acting on the loop is
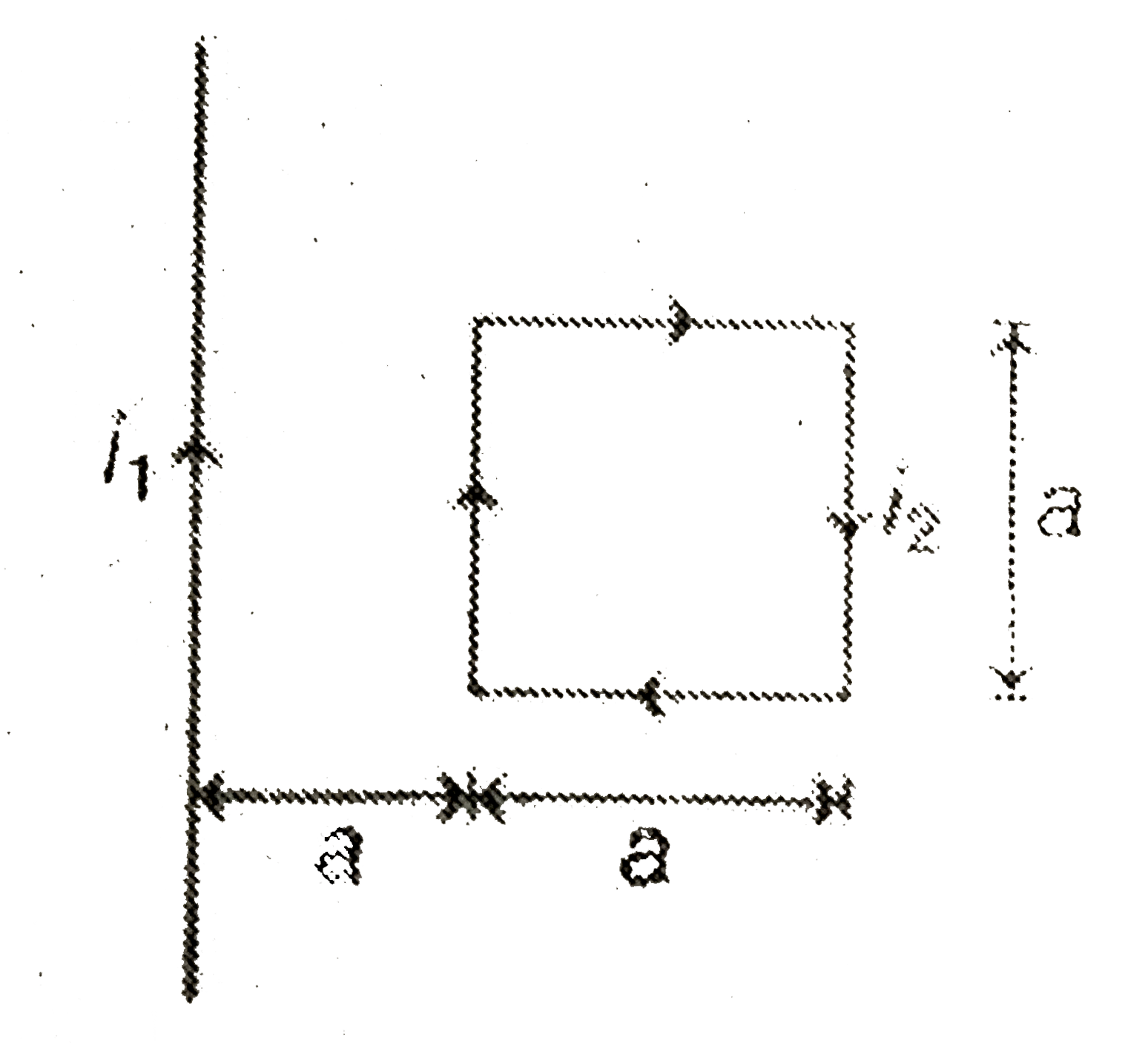
View SolutionTwo identical pieces of metal wires are used to make a circular loop and a square loop same current is passed through both the loops what is the ratio of magneitc dipole moment associated with the circular loop that of the square loop ?
View SolutionA current carrying squre loop is placed near an infinitely long current carrying wire as shown in figure . The loop torque acting on the loop is

View Solution