Do magnetic forces obey Newton's third law. Verify for two current elements d→l1=dlˆi located at the origin and d→l2=dlˆj located at (0, R, 0). Both carry current I.
In Biot-savart's law, magnetic field B is parallel (II) to ×r and idl have its direction along the direction of flow of current.
Here. For the direction of magnetic field At dl2, located at (0,R,0) due to wire d1 is given by B∣∣×r or ˆi׈j (because poiint (0,R,0) lies on y-axis), but ˆi׈j=ˆk
So, the direction of magnetic field at d2 is along z-direction.
The direction of magnetic force exerted at d2 because of the first wire along the x-axis F=i(I×B) i.e., F∣∣(i×k) or along −ˆj direction.
Therefore, force due to dl1 on dl2 is non-zero.
Now, for the direction of magnetic field At d1, located at (0,0,0) due to wire d2 is given by B∣∣×r or ˆj×−ˆj (because origiin lies on y-direction w.r.t. point (0,R,0), but j×−ˆj=0
So, the magnetic field at d1 does not exist.
Force due to dl2 on dl1 is zero.
So, magnetic forces do not obey newton's third law.
Topper's Solved these Questions
Similar Questions
State the Biot-Savart's law for the magnetic field due to a current carrying element. Use this law to obtain a formula for magnetic field at the centre of a circular loop of radius R carrying a steady current I, sketch the magnetic field lines for a current loop clearly indicating the direction of the field.
View SolutionHow will the conductor, carrying current I0 rotate immediately after it is released in following three cases [consider magnetic force only]
(a) Conductor carrying current I0 is placed symmetrically above poles of a fixed U shaped magnet (figure a).
(b) Conductor carrying current I0 is placed symmetrically at a distance from a fixed current (I1) carrying wire (fig. (b))
(c) An insulated circular current carrying wire is held fixed in vertical plane. Conductor carrying current I0 is in the shape of a circle of diameter nearly equal to that of the fixed insulated circle. The planes of the two circles are perpendicular to each other (fig. (c)) with xy as common diameter


View Solution
Knowledge Check
The magnetic field d→B due to a small current element d→l at a distance →r and element carrying current i is,
Ad→B=μ04πi(d→l×→rr)Bd→B=μ04πi2(d→l×→rr)Cd→B=μ04πi2(d→l×→rr2)Dd→B=μ04πi(d→l×→rr3)Two point charges are fixed on the Xaxis , q1=12.0mC is located at the origin and q2=−3.0mC is located at point A, with x2=8.0cm. Where should a third charge q3, be placed on the X-axis so that the total, electrostatic force acting on it is zero?
Aat x3=16cmBat x3=12cmCat x3=24cmDat x3=6cmThere are two straight conductors, carrying currents i1 and i2. Both the conductors are kept parallel to each other at a separation 2d. The magnetic field is measured at a point midway between the conductors. Magnetic field intensity at the above specified point is 20μT when both the wire carry current in the same direction but it becomes 80μT when the current in one of them is reversed. Assume i1>i2 and find i1/i2.
A2B5/3C4D7/3
. A small circular ring of radius R is placed in Y-Z plane with its centre at (−a,0,0). Another small circular ring of same radius Ris placed in X-Z plane with its centre at(0,−a,0). Calculate the magnitude and direction of net magnetic field at the origin (0, 0, 0), if both the rings carry current I. The direction of current in the first loop and the second loop is clockwise and anticlockwise respectively, when seen from the origin.
View SolutionTwo infinitely long straight wires lie in the xy-plane along the lines x=±R. The wire located at x=+R carries a constant current I1 and the wire located at x=−R carries a constant current I2. A circular loop of radius R is suspended with its centre at (0,0,√3R) and in a plane parallel to the xy-plane. This loop carries a constant current ? in the clockwise direction as seen from above the loop. The current in the wire is taken to be positive if it is in the +ˆJ direction. Which of the following statements regarding the magnetic field →B is (are) true?
View SolutionA current circular conducting loop exerts a magnetic field both inside and outside it. The magnetic field at the cetre of a current loop of radius 'R' and carrying a current I is given as :
B=μ0I2R
The magnetic field lines due to a circular current loop form closed loops. The direction of the magnetic field is given by the right hand thumb rule, which states that if one curls the palm of his right hand around the current loop with the fingers pointing in the direction of the current, the right hand thumb will give the direction of the magnetic field. From this law it is clear that the direction of magnetic field →B is always perpendicular to the direction of flow of current or perpendicular to the plane of circular current loop.
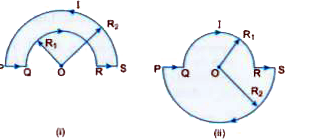
Determine the magnetic field at the centre point O due to two concentric semicircular loops of radii R1andR2 carrying a current I, when the loops of radii R1andR2 carrying a current I, when the loops are arranged as shown in Fig.
View SolutionA current element of length 0.1 cm is placed along northsouth direction and carries a current of 5 A from south to north. Find the magnetic field due to the current element at a point located at a distance of 150 cm from it towards east.
View SolutionThe magnetic field at a distance r from a long wire carrying current i is 0.4 T. The magnetic field at a distance 2r is
View Solution
