Doubtnut Promotions Sticky

The number of real solutions of tan−1√x(x+1)+sin−1√x2+x+1=π2 is (a) zero b. one c. two d. infinite

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:N/a

We have, tan−1√x(x+1)+sin−1√x2+x+1=π2.......(i)
Let sin−1√x2+x+1=θ
⇒sinθ=√x2+x+11
⇒tanθ=√x2+x+1√−x2−x
∵θ=tan−1'√x2+x+1√−x−x
=sin−1√x2+x+1
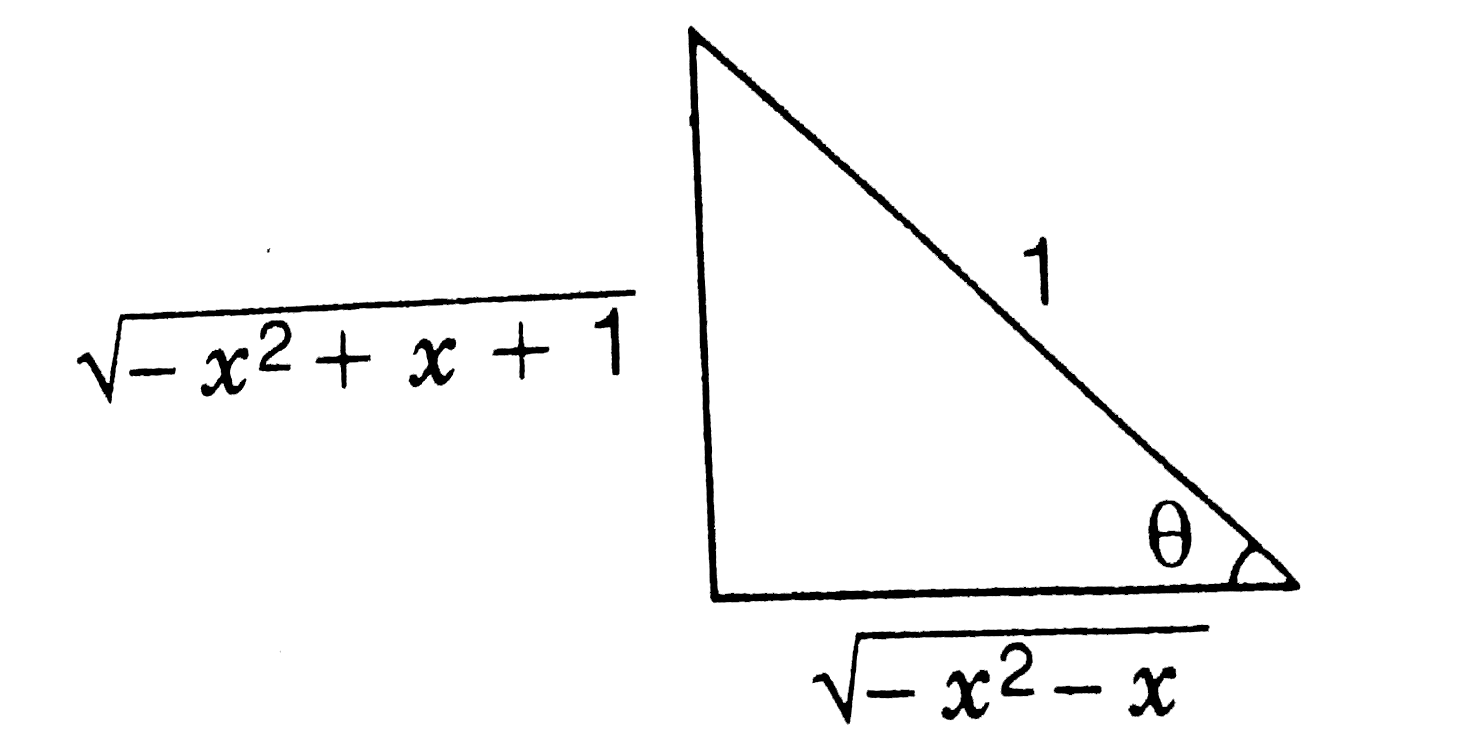
ocr_image
On putting the value of θ in Eq. (i), we get
tan−1√x(x+1)+tan−1'√x2+x+1√−x2−x=π2
We know that, tan−1x+tan−1y=tan−1(x+y1−xy),xy<1
∴tan−1⎡⎢ ⎢ ⎢ ⎢⎣√x(x+1)+√x2+x+1−x2−x1−√x(x+1).√x2+x+1−x2−x⎤⎥ ⎥ ⎥ ⎥⎦=π2
⇒tan−1⎡⎢ ⎢ ⎢ ⎢⎣√x2+x+√x2+x+1−1(x2+x)1−√(x2+x).(x2+x+1)−1(x2+x)⎤⎥ ⎥ ⎥ ⎥⎦=π2
⇒x2+x+√−(x2+x+1)[1−√−(x2+x+1)]√(x2+x)=tan'π2=10
⇒[1−√−(x2+x+1)]√(x2+x)=0
⇒−(x2+x+1)=1 or x2+x=0
⇒−x2−x−1=1 or x(x+1)=0
⇒x2+x+2=0 or x(x+1)=0
∴x=−1±√1−4×22
⇒x=0 or x=−1
For real solution, we have x=0,−1.

|