If the vertex of a parabola is the point (−3,0) and the directrix is the line x+5=0, then find its equation.
A
y2=8(x+3)
B
x2=8(y+3)
C
y2=−8(x+3)
D
y2=8(x+5)
Video Solution
Text Solution
The correct Answer is:A
Here, vertex=(-3,0)
∴a=-3 and directrix,x+5=0
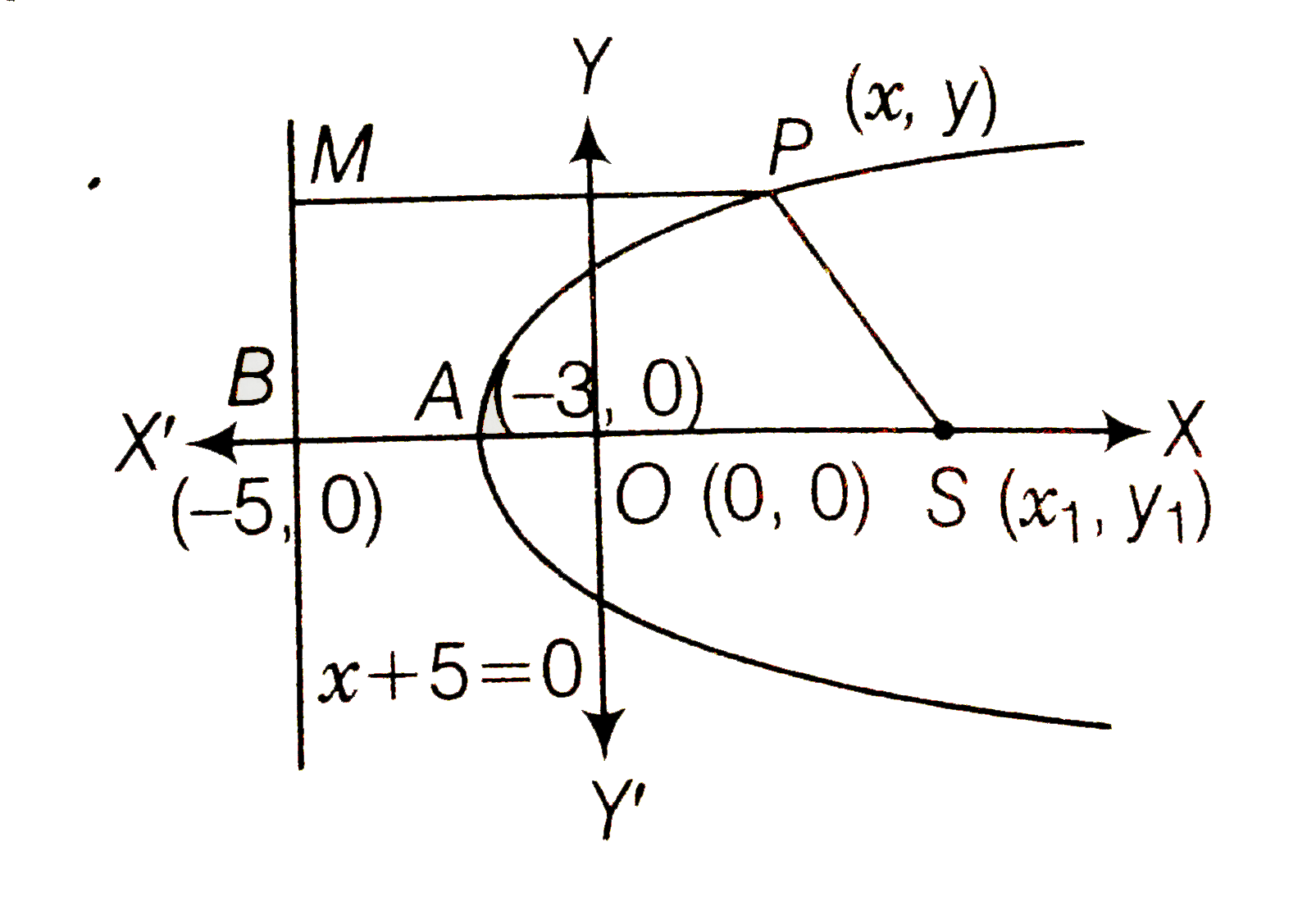
Since, axis of the parabola is a line perpendicular to directrix and A is the midpoint of AS
Then −3=x1−52
⇒−6=x1−5⇒x1=−1
0=0+y12⇒y1=0
∴S=(−1,0)
∵PM=PS
⇒|x+5|=√(x+1)2+y2
⇒x2+2x+1+y2=x2+10x+25
⇒y2=+8x+24
⇒y2=+8(x+3)
|
Topper's Solved these Questions
- CONIC SECTIONSBook:NCERT EXEMPLARChapter:CONIC SECTIONSExercise:Fillers
Explore 6 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBook:NCERT EXEMPLARChapter:COMPLEX NUMBERS AND QUADRATIC EQUATIONSExercise:OBJECTIVE TYPE QUESTIONS
Explore 16 Videos
- INTRODUCTION TO THREE DIMENSIONAL GEOMETRYBook:NCERT EXEMPLARChapter:INTRODUCTION TO THREE DIMENSIONAL GEOMETRYExercise:Fillers
Explore 16 Videos
Similar Questions
Knowledge Check
If the vertex of a parabola is the point (−3,0) and the directrix is the line x+5=0, then its equation is
Ay2=8(x+3)Bx2=8(y+3)Cy2=−8(x+3)Dy2=8(x+5)If the vertex of a parabola is (0,2), directrix on x-axis then its focus is :
A(0,0)B(0,4)C(4,0)DNone of these.The equation of the parabola with the focus (3,0) and directrix x+3=0 is
Ay2=2xBy2=3xCy2=6xDy2=12x
The equation of the parabola whose focus is (−3,0) and the directrix is,x+5=0 is:
View SolutionThe equation of the parabola whose focus is (-3,0) and the directrix is x+5=0 is:
View SolutionFind the equation of the parabola with focus at F(3,0) and the directrix x=-3.
View SolutionAn equation of the parabola whose focus is (−3,0) and the directrix is x +5=0 is :
View SolutionIf the focus of a parabola is (0,−3) and its directrix is y=3, then its equation is
View Solution