Find the equation of the circle which touches both the axes and the line 3x−4y+8=0 and lies in the third quadrant.
A
x2+y2−4x−4y+4=0
B
x2+y2+4x+4y+4=0
C
x2+y2+2x+2y+4=0
D
none of these
Video Solution
Text Solution
The correct Answer is:B
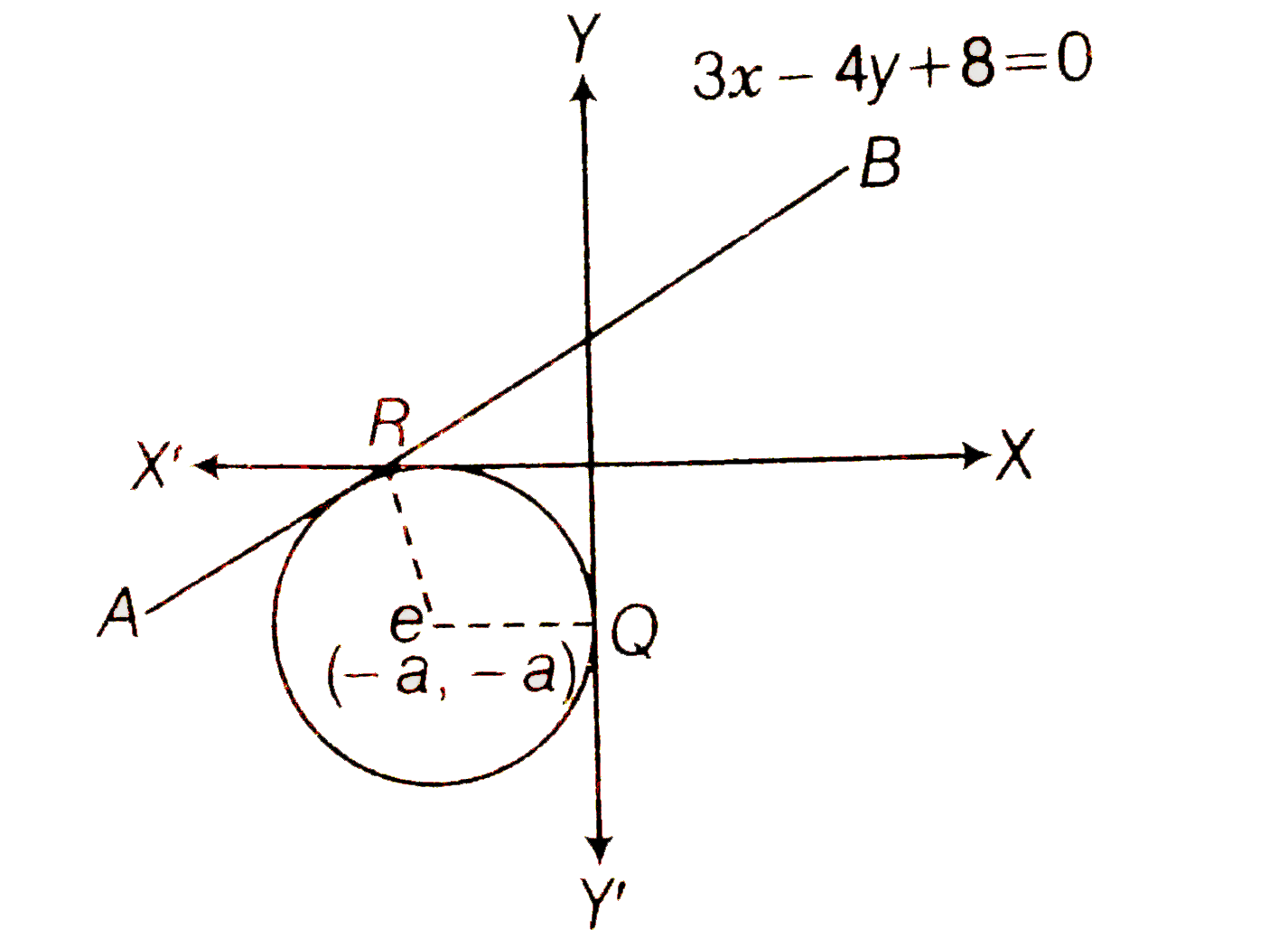
Let a be the radius of the circle. Then, the coordinates of the circle are (-a, -a). Now perpendicular distance from C to the line AB = Radius of the circle
d=∣∣∣−3a+4a+8√9+16∣∣∣=∣∣∣a+85∣∣∣
∵a=±(a+85)
Taking positive sign, a=a+85
⇒ 5a=a+8
⇒ 4a=8 ⇒a=2
Taking negative sign, a=−a−85
⇒ 5a=−a−8
⇒ 6a=−8 ⇒ a=−43
But a≠ −43
∵ a=2
So, the equation of the circle is
(x+2)2+(y+2)2=22
⇒x2+4x+4+y2+4y+4=4
⇒x2+y2+4x+4y+4=0
|
Topper's Solved these Questions
- CONIC SECTIONSBOOK - NCERT EXEMPLARCHAPTER - CONIC SECTIONSEXERCISE - Long answer
10 Videos
- CONIC SECTIONSBOOK - NCERT EXEMPLARCHAPTER - CONIC SECTIONSEXERCISE - True/False
8 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - NCERT EXEMPLARCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - OBJECTIVE TYPE QUESTIONS
16 Videos
- INTRODUCTION TO THREE DIMENSIONAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - INTRODUCTION TO THREE DIMENSIONAL GEOMETRYEXERCISE - Fillers
16 Videos
Similar Questions
Knowledge Check
Find the equation of a circle which touches both the axes and the line 3 4 8 0 x y - + = and lies in the third quadrant.
Ax2+y2+4x+4y−4=0Bx2+y2−4x−4y+4=0Cx2+y2+4x+4y+4=0DNone of the aboveThe equations of the circles which touch both the axes and the line x = a are
Ax2+y2±ax±ay+a24=0Bx2+y2+ax±ay+a24=0Cx2+y2−ax±ay+a24=0Dnone of theseThe equation of the circles which touch both the axes and the line 4x+3y=12 and have centres in the first quadrant, are
Ax2+y2−x−y+1=0Bx2+y2−2x−2y+1=0Cx2+y2−12x−12y+36=0Dx2+y2−6x−6y+36=0
Equation of circles which touch both the axes and also the line x=k(k>0) is
View SolutionFind the equation of the circle which touches the lines x=0 ,y=0 and x=c
View SolutionFind the equation of the circle which touches both the axes and the straight line 4x+3y=6 in the first quadrant and lies below it.
View SolutionFind the equation of the circle which touches the coordinate axes and whose centre lies on the line x−2y=3.
View SolutionFind the equation of the circle which touches the lines x=0,y=0andx=4 and lies in the first quadrant.
View Solution