Let circles C1,C2andC3 with centres O1,O2andO3 respectively touch each other externally, where
O1=(−36,7),O2=(20,7)andO3=(0,−8). The coordinates of the centre of a circle passing through the points of contact of circles C1,C2andC2,C3andC3,C1 are
(−1,0)
(1,0)
(0,1)
(0,−1)
The correct Answer is:A
To find the coordinates of the center of a circle that passes through the points of contact of circles C1,C2 and C2,C3 and C3,C1, we need to determine the incenter of triangle formed by the centers of these circles O1,O2,O3.
Step 1: Identify the coordinates of the centers
The centers of the circles are given as:
- O1=(−36,7)
- O2=(20,7)
- O3=(0,−8)
Step 2: Calculate the lengths of the sides of triangle O1O2O3
Using the distance formula d=√(x2−x1)2+(y2−y1)2:
1. Length O1O2:
O1O2=√(20−(−36))2+(7−7)2=√(20+36)2=√562=56
2. Length O2O3:
O2O3=√(0−20)2+(−8−7)2=√(−20)2+(−15)2=√400+225=√625=25
3. Length O3O1:
O3O1=√(−36−0)2+(7−(−8))2=√(−36)2+(7+8)2=√1296+225=√1521=39
Step 3: Use the lengths to find the incenter
The incenter I of triangle O1O2O3 can be calculated using the formula:
Ix=a⋅x1+b⋅x2+c⋅x3a+b+c
Iy=a⋅y1+b⋅y2+c⋅y3a+b+c
where a,b,c are the lengths of the sides opposite to vertices O1,O2,O3 respectively.
Assigning:
- a=O2O3=25
- b=O3O1=39
- c=O1O2=56
Coordinates:
- O1=(−36,7)
- O2=(20,7)
- O3=(0,−8)
Calculating Ix:
Ix=25⋅(−36)+39⋅20+56⋅025+39+56=−900+780+0120=−120120=−1
Calculating Iy:
Iy=25⋅7+39⋅7+56⋅(−8)25+39+56=175+273−448120=0120=0
Step 4: Conclusion
The coordinates of the center of the circle passing through the points of contact of circles C1,C2, C2,C3, and C3,C1 is:
(−1,0)
The centers of the circles are given as:
- O1=(−36,7)
- O2=(20,7)
- O3=(0,−8)
Using the distance formula d=√(x2−x1)2+(y2−y1)2:
O1O2=√(20−(−36))2+(7−7)2=√(20+36)2=√562=56
O2O3=√(0−20)2+(−8−7)2=√(−20)2+(−15)2=√400+225=√625=25
O3O1=√(−36−0)2+(7−(−8))2=√(−36)2+(7+8)2=√1296+225=√1521=39
The incenter I of triangle O1O2O3 can be calculated using the formula:
Ix=a⋅x1+b⋅x2+c⋅x3a+b+c
Iy=a⋅y1+b⋅y2+c⋅y3a+b+c
where a,b,c are the lengths of the sides opposite to vertices O1,O2,O3 respectively.
- a=O2O3=25
- b=O3O1=39
- c=O1O2=56
- O1=(−36,7)
- O2=(20,7)
- O3=(0,−8)
Ix=25⋅(−36)+39⋅20+56⋅025+39+56=−900+780+0120=−120120=−1
Iy=25⋅7+39⋅7+56⋅(−8)25+39+56=175+273−448120=0120=0
The coordinates of the center of the circle passing through the points of contact of circles C1,C2, C2,C3, and C3,C1 is:
(−1,0)
Topper's Solved these Questions
Similar Questions
Three circles with centres C1,C2andC3 and radii r1,r2andr3 where r1<r2<r3 are placed as shown in the figure
View SolutionThe circle S1 with centre C1(a1,b1) and radius r1 touches externally the circle S2 with centre C2(a2,b2) and radius r2 If the tangent at their common point passes through the origin, then
View Solution
Knowledge Check
C3H6O2
 ACH3−CH2−COOHB
ACH3−CH2−COOHB CCH3−CO−CH2−OHD
CCH3−CO−CH2−OHD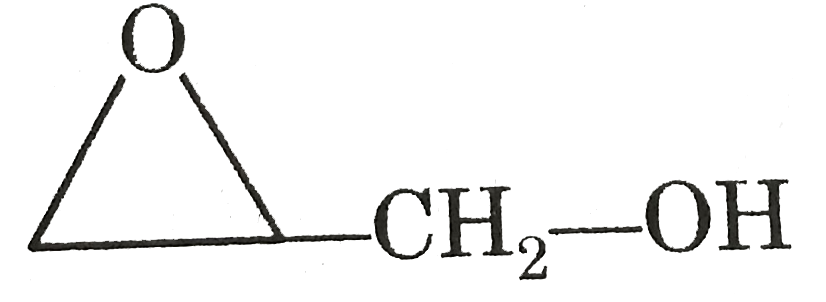
In C3O2, the hybridization state of carbon is :
AspBsp2Csp3Ddsp3Three circles whose radii are 2, 3, 4 units and having centres as C1,C2,C3 respectively touch each other externally at D,E,F. The circumradius of triangle DEF is :
A2√63B4√63C√63DNone
C1andC2 are fixed circles of radii r1andr2 touches each other externally. Circle 'C' touches both Circles C1andC2 extemelly. If r1r2=32 then the eccentricity of the locus of centre of circles C is
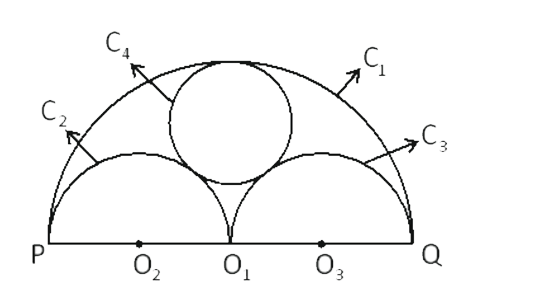
View SolutionIn the figure PQ PO1andO1Q are the diameters of semicircles C1,C2andC3 with centres at O1,O2andO3 respectively C1C2andC3 . If PQ = 24 units and the area of the circle C4 is A sq. units , then the value of 8π4 is equal ot (here, PO1=O1Q)
View SolutionA circle C1 has radius 2 units and a circles C2 has radius 3 units. The distance between the centres of C1 and C2 is 7 units. If two points, one tangent to both circles and the other passing through the centre of both circles, intersect at point P which lies between the centers of C1andC2, then the distance between P and the centre of C2 is
View SolutionTwo circles of radii 8 cm and 2 cm respectively touch each other externally at the point A. PQ is the direct common tangent of these two circles of centres O1andO2 respectively. The length of PQ is equal to :
View SolutionThe compounds CH3−O−C3H7 and C2H5−O−C2H5 exhibit
View Solution
