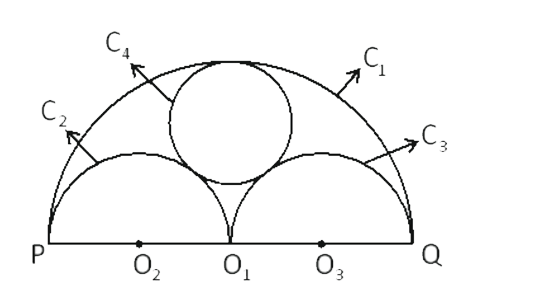
In the figure PQ PO1andO1Q are the diameters of semicircles C1,C2andC3 with centres at O1,O2andO3 respectively C1C2andC3 . If PQ = 24 units and the area of the circle C4 is A sq. units , then the value of 8π4 is equal ot (here, PO1=O1Q)
The correct Answer is:0.5
Step by step video, text & image solution for In the figure PQ PO_1 and O_1Q are the diameters of semicircles C_1,C_2 and C_3 with centres at O_1 ,O_2 and O_3 respectively C_1 C_2 and C_3 . If PQ = 24 units and the area of the circle C_4 is A sq. units , then the value of (8pi)/(4) is equal ot (here, PO_1 = O_1Q) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The circle C1:x2+y2=3, with centre at O, intersects the parabola x2=2y at the point P in the first quadrant. Let the tangent to the circle C1 at P touches other two circles C2andC3atR2andR3, respectively. Suppose C2andC3 have equal radii 2√3 and centres at Q2 and Q3 respectively. If Q2 and Q3 lie on the y-axis, then (a)Q2Q3=12(b)R2R3=4√6(c)area of triangle OR2R3 is 6√2 (d)area of triangle PQ2Q3is=4√2
View SolutionThe line L1≡3x−4y+1=0 touches the circles C1andC2. Centers of C1 and C2 are A1(1,2) and A2(3,1) respectively Then, the length (in units) of the transverse common tangent of C1andC2 is equal to
View Solution
Knowledge Check
In, the charges on C1,C2, and C3, are Q1,Q2, and Q3, respectively.
 .AQ2=8μCBQ3=12μCCQ1=20μCDQ2=12μC
.AQ2=8μCBQ3=12μCCQ1=20μCDQ2=12μCC1andC2 are two concentric circles with centres at O. Their radii are 12 cm and 3 cm respectively. B and C are the points of contact of two tangents draw to C2 from a point A lying on the circle C1. Then the area of the quadrilateral ABOC is-
A9√152cm2B12√15cm2C9√15cm2D6√15cm2C is the mid-point of PQ, if P is (4, x), C is (y, -1) and Q is (-2, 4), then x and y respectively are
A- 6 and 1B- 6 and 2C6 and - 1D6 and - 2
Three capacitors C1,C2 and C3 are connected as shown in, The potentials of P,Q, and R are V1,V2, and V3, respectively. Find the potential V0 at the functionO.
 .
.
View SolutionLet circles C1,C2andC3 with centres O1,O2andO3 respectively touch each other externally, where
O1=(−36,7),O2=(20,7)andO3=(0,−8). The coordinates of the centre of a circle passing through the points of contact of circles C1,C2andC2,C3andC3,C1 are
View SolutionA circle C1 of radius 2 units rolls o the outerside of the circle C2:x2+y2+4x=0 touching it externally.
The locus of the centre of C1 is
View SolutionThe circle C1:x2+y2=3, with cenre at O, intersects the parabola x2=2y at the point P in the first quadrant. Let the tangent to the circle C1 at P touches other two circles C2 and C3 at R2 and R3 respectively. Suppose C2 and C3 have equal radii 2√3 and centres Q2 and Q3 respectively. If Q2 and Q3 lie on the y-axis, then Q2Q3=
View SolutionTwo circles of radii 8 cm and 2 cm respectively touch each other externally at the point A. PQ is the direct common tangent of these two circles of centres O1andO2 respectively. The length of PQ is equal to :
View Solution

