Line L1≡3x−4y+1=0 touches the cirlces C1andC2. Centres of C1andC2 are A2(1,2)andA2(3,1) respectively, then identify the INCORRECT statement from the following statements.
L1 is direct common tangent of these circles
L1 is transverse common tangent to these circles
Radius of circle C1 is 45 units
Radius of circle C2 is 65 units
The correct Answer is:A
To solve the problem step by step, we need to analyze the given line and the circles, and then determine which statement is incorrect.
Step 1: Identify the given line and circles
The line is given by the equation:
L1:3x−4y+1=0
The centers of the circles are:
- Circle C1 with center A1(1,2)
- Circle C2 with center A2(3,1)
Step 2: Determine the type of tangent
The problem states that the line L1 touches both circles. We need to determine if it is a direct common tangent or a transverse common tangent.
- Direct Common Tangent (DCT): A tangent that touches both circles on the same side.
- Transverse Common Tangent (TCT): A tangent that touches both circles on opposite sides.
Step 3: Calculate the distance from the centers to the line
We will use the formula for the distance d from a point (x1,y1) to a line ax+by+c=0:
d=|ax1+by1+c|√a2+b2
For Circle C1 at A1(1,2):
- a=3,b=−4,c=1
d1=|3(1)−4(2)+1|√32+(−4)2=|3−8+1|√9+16=|−4|5=45
For Circle C2 at A2(3,1):
d2=|3(3)−4(1)+1|√32+(−4)2=|9−4+1|5=|6|5=65
Step 4: Identify the radii of the circles
Since the line is a tangent to both circles, the distances calculated above represent the radii of the circles:
- Radius of circle C1 is R1=45
- Radius of circle C2 is R2=65
Step 5: Analyze the statements
Now we need to analyze the statements regarding the tangents and the radii:
1. Statement A: L1 is a Direct Common Tangent of Circles.
2. Statement B: L1 is a Transverse Common Tangent of Circles.
3. Statement C: Radius of C1 is 45 units.
4. Statement D: Radius of C2 is 65 units.
Step 6: Determine the incorrect statement
From our analysis:
- Since the line L1 touches the circles on opposite sides, it is a Transverse Common Tangent (Statement B is correct).
- The radii calculated are correct (Statements C and D are correct).
- Therefore, Statement A is incorrect.
Final Answer
The incorrect statement is:
A. L1 is a Direct Common Tangent of Circles.
The line is given by the equation:
L1:3x−4y+1=0
The centers of the circles are:
- Circle C1 with center A1(1,2)
- Circle C2 with center A2(3,1)
The problem states that the line L1 touches both circles. We need to determine if it is a direct common tangent or a transverse common tangent.
- Transverse Common Tangent (TCT): A tangent that touches both circles on opposite sides.
We will use the formula for the distance d from a point (x1,y1) to a line ax+by+c=0:
d=|ax1+by1+c|√a2+b2
- a=3,b=−4,c=1
d1=|3(1)−4(2)+1|√32+(−4)2=|3−8+1|√9+16=|−4|5=45
d2=|3(3)−4(1)+1|√32+(−4)2=|9−4+1|5=|6|5=65
Since the line is a tangent to both circles, the distances calculated above represent the radii of the circles:
- Radius of circle C1 is R1=45
- Radius of circle C2 is R2=65
Now we need to analyze the statements regarding the tangents and the radii:
1. Statement A: L1 is a Direct Common Tangent of Circles.
2. Statement B: L1 is a Transverse Common Tangent of Circles.
3. Statement C: Radius of C1 is 45 units.
4. Statement D: Radius of C2 is 65 units.
From our analysis:
- Since the line L1 touches the circles on opposite sides, it is a Transverse Common Tangent (Statement B is correct).
- The radii calculated are correct (Statements C and D are correct).
- Therefore, Statement A is incorrect.
The incorrect statement is:
A. L1 is a Direct Common Tangent of Circles.
Topper's Solved these Questions
Similar Questions
The line L1≡3x−4y+1=0 touches the circles C1andC2. Centers of C1 and C2 are A1(1,2) and A2(3,1) respectively Then, the length (in units) of the transverse common tangent of C1andC2 is equal to
View SolutionThe lines a1x+b1y+c1=0 and a2x+b2y+c2=0 are perpendicular to each other , then _______.
View Solution
Knowledge Check
If the lines x=a1y+b1,z=c1y+d1 and x=a2y+b2,z=c2y+d2 are perpendicular, then
Aa1a2+b1b2+1=0Ba1a2+c2c2+1=0Ca1a2+b1b2=0Da1c2+b1c1=0Three rectangles A1,A2 and A3 have the same area Their lengths a1,a2 and a3 respectively are such that a1<a2<a3. Cylinders C1,C2 and C3 are formed from A1,A2 and A3 respectively by joining the parallel sides along the breadth. Then,
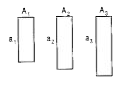 AC1 will enclose maximum volumeBC2 will enclose maximum volumeCC3 will enclose maximum volumeDEach of C1,C2 and C3 will enclose equal volume.
AC1 will enclose maximum volumeBC2 will enclose maximum volumeCC3 will enclose maximum volumeDEach of C1,C2 and C3 will enclose equal volume.Let each of the circles
S1≡x2+y2+4y−1=0
S1≡x2+y2+6x+y+8=0
S3≡x2+y2−4x−4y−37=0
touch the other two. Also, let P1,P2 and P3 be the points of contact of S1 and S2,S2 and S3, and S3 , respectively, C1,C2 and C3 are the centres of S1,S2 and S3 respectively.
P2 and P3 are images of each other with respect to the lineAy=xBy=−xCy=x+1Dy=−x+2
The lines a1x+b1y+c1=0 and a2x+b2y+c2=0 are perpendicular to each other , then _______.
View SolutionLet the incircle of ΔABC touches the sides BC, CA, AB at A1,B1,C1 respectively. The incircle of ΔA1B1C1 touches its sides of B1C1,C1A1andA1B1 at A2,B2,C2 respectively and so on.
Q. In ΔA4B4C4, the value of ∠A4 is:
View SolutionLet the incircle of ΔABC touches the sides BC, CA, AB at A1,B1,C1 respectively. The incircle of ΔA1B1C1 touches its sides of B1C1,C1A1andA1B1 at A2,B2,C2 respectively and so on.
Q. In ΔA4B4C4, the value of ∠A4 is:
View SolutionStatement - 1 : For the straight lines 3x - 4y + 5 = 0 and 5x + 12 y - 1 = 0 , the equation of the bisector of the angle which contains the origin is 16 x + 2 y + 15 = 0 and it bisects the acute angle between the given lines .
statement - 2 : Let the equations of two lines be a1x+b1y+c1=0 and a2x+b2y+c2=0 where c1 and c2 are positive . Then , the bisector of the angle containing the origin is given by
a1x+b1y+c1√a22+b21=a2x+b2y+c2√a22+b22
If a1a2+b1b2>0 , then the above bisector bisects the obtuse angle between given lines .
View SolutionLet C1,C2 be two circles touching each other externally at the point A and let AB be the diameter of circle C1. Draw a secant BA3 to circle C2, intersecting circle C1 at a point A1(≠A), and circle C2 at points A2 and A3 . If BA1=2, BA2=3 and BA3=4, then the radii of circles C1 and C2 are respectively
View Solution
