Let $C_{1}, C_{2}$ be two circles touching each other externally at the point A and let AB be the diameter of circle $C_{1}$ . Draw a secant $B A_{3}$ to circle $C_{2}$ , intersecting circle $C_{1}$ at a point $A_{1} (\neq A),$ and circle $C_{2}$ at points $A_{2}$ and $A_{3}$ . If $B A_{1} = 2$ , $B A_{2} = 3$ and $B A_{3} = 4$ , then the radii of circles $C_{1}$ and $C_{2}$ are respectively

A

$\frac{\sqrt{30}}{5}, \frac{3 \sqrt{30}}{10}$

B

$\frac{\sqrt{5}}{2}, \frac{7 \sqrt{5}}{10}$

C

$\frac{\sqrt{6}}{2}, \frac{\sqrt{6}}{2}$

D

$\frac{\sqrt{10}}{3}, \frac{17 \sqrt{10}}{30}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

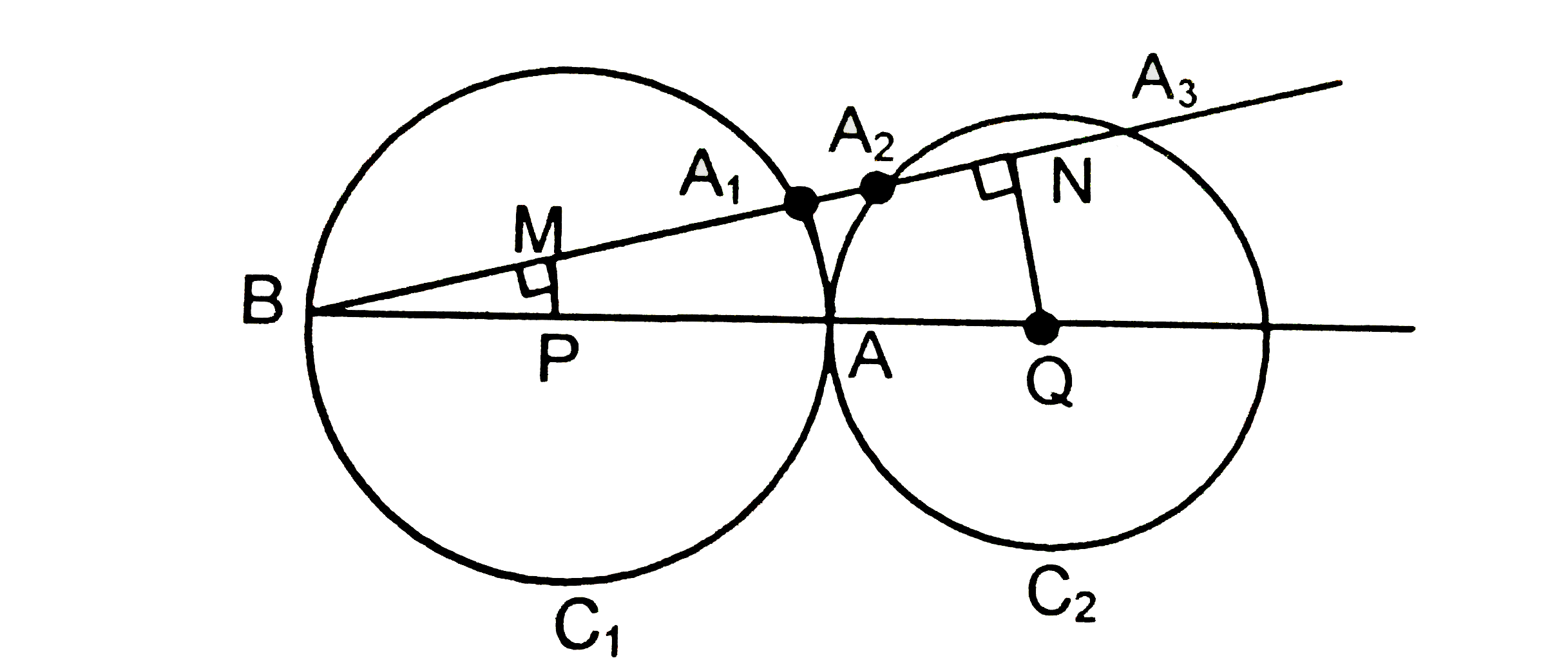
$B M = A_{1} M = 1$
$A_{1} A_{2} = 1$
$Let radius of C_{1} is r_{1}$
$Let radius of C_{2} is r_{2}$
$P M = \sqrt{r_{1}^{2} - 1}, Q N = \sqrt{r_{2}^{2} - \frac{1}{4}}$
$∵ △ Q N B ~ △ P M B$
$∴ \frac{\sqrt{r_{2}^{2} - \frac{1}{4}}}{\sqrt{r_{1}^{2} - 1}} = \frac{B N}{B M} = \frac{7 / 2}{1}$
$\Rightarrow 4 r_{2}^{2} = 49 r_{1}^{2} - 48 ... (i)$
$Also, in △ Q N B$
$B Q^{2} = B N^{2} + N Q^{2}$
${(2 r_{1} + r_{2})}_{1}^{2} = \frac{49}{4} + r_{2}^{2} - \frac{1}{4}$
$r_{1}^{2} + r_{1} r_{2} = 3$
$Solve(i) & (ii)$
$r_{1} = \sqrt{\frac{6}{5}} = \frac{\sqrt{30}}{5} & r_{2} = \frac{3 \sqrt{30}}{10}$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Circles C(o, r) and $C (O^{1}, \frac{r}{2})$ touch internally at a point A and AB is a chord of the circle intersecting $C (O^{1}, \frac{r}{2})$ at C. Then AC is equal to :
ACB
BOA
COB
D $\frac{1}{3}$ AB
Question 2 - Select One
The circle $C_{1} : x^{2} + y^{2} = 3$ , with cenre at O, intersects the parabola $x^{2} = 2 y$ at the point P in the first quadrant. Let the tangent to the circle $C_{1}$ at P touches other two circles $C_{2}$ and $C_{3}$ at $R_{2}$ and $R_{3}$ respectively. Suppose $C_{2}$ and $C_{3}$ have equal radii $2 \sqrt{3}$ and centres $Q_{2}$ and $Q_{3}$ respectively. If $Q_{2}$ and $Q_{3}$ lie on the y-axis, then $Q_{2} Q_{3} =$
A3
B6
C9
D12

KVPY PREVIOUS YEAR-KVPY-Part 2 Mathematics

Home
Ask Doubt
Profile