Find the x coordinate of the centre of mass of the non - uniform rod of length L givne below. The origin is taken at the left end of the rod. The density of the rod as a function of its x- coordinates is ρ=ax2+bx+c, where a, b and c are constants.

2aL2+3bL2+6cL2(3aL2+4bL+8c)
4aL3+3bL2+2cL2(3aL2+2bL+c)
3aL2+4bL2+2cL4aL2+6bL+8c
3aL3+4bL2+6cL2(2aL2+3bL+6c)
The correct Answer is:D
Step by step video, text & image solution for Find the x coordinate of the centre of mass of the non - uniform rod of length L givne below. The origin is taken at the left end of the rod. The density of the rod as a function of its x- coordinates is rho=ax^(2)+bx+c, where a, b and c are constants. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Find coordinates of mass center of a non-uniform rod of length L whose linear mass density lambda varies as lambda=a+bx, where x is the distance from the lighter end.
View SolutionThe centre of mass of a non-uniform rod of length L whose mass per unit length λ is proportional to x2, where x is distance from one end

View Solution
Knowledge Check
The mass per unit length of a non-uniform rod of length L is given by μ=λ×2, where λ is a constant and x is distance from one end of the rod. The distance of the center of mass of rod from this end is :-
AL2BL4C3L4DL3The mass per unit length of a non - uniform rod of length L is given μ=λx2 , where λ is a constant and x is distance from one end of the rod. The distance of the center of mas of rod from this end is
AL2BL4C3L4DL3The density of a non-uniform rod of length 1m is given by ρ(x)=a(1+bx2) where, a and b are constant and 0≤x≤1. The centre of mass of the rod will be at
A3(2+b)4(3b+b)B4(2+b)3(3+b)C3(3+b)4(2+b)D4(3+b)3(2b+b)
The y co - ordinate of the centre of mass of the system of three rods of length 2a and two rods of length a as shown in the figure is (Assume all rods to be of uniform density)
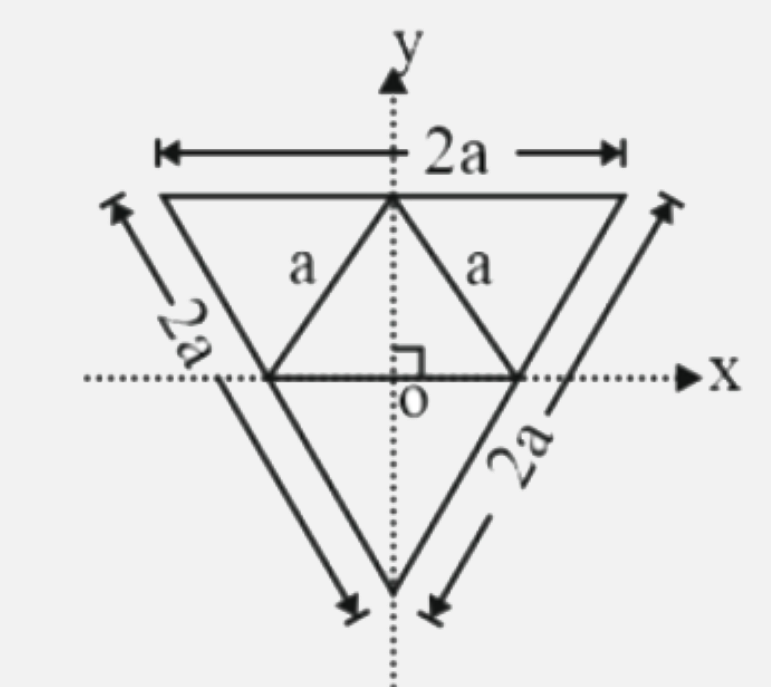
View SolutionThe density of a linear rod of length L varies as ρ=A+Bx where x is the distance from the left end. Locate the centre of mass.

View SolutionA rod of length l is pivoted about an end . Find the moment of inertia of the rod about this axis if the linear mass density of rod varies as ρ=ax2+b kg/m
View SolutionThe ends of a rod of length k moves on two positive coordinate axes.The locus of the point on the rod,which divides it in the ratio l:m is
View SolutionThe linear density of a non−uniform rod of length 2m is given by λ(x)=a(1+bx2) where a and b are constants and 0≤x≤2. The centre of mass of the rod will be at. X=
View Solution