A person has undertaken a construction job. The probabilities are 0.65 that there will be strike. 0.80 that the construction job will be completed on time if there is no strike, and 0.32 that the construction job will be completed on time if there is a strike. Determine the probability that the construction job will be completed on time.
To determine the probability that the construction job will be completed on time, we can use the law of total probability. Let's denote:
- B: the event that there is a strike.
- A: the event that the construction job is completed on time.
We are given the following probabilities:
1. P(B)=0.65 (the probability that there will be a strike).
2. P(A|B′)=0.80 (the probability that the job is completed on time given that there is no strike).
3. P(A|B)=0.32 (the probability that the job is completed on time given that there is a strike).
We need to find P(A), the total probability that the construction job will be completed on time. According to the law of total probability:
P(A)=P(B)⋅P(A|B)+P(B′)⋅P(A|B′)
Where P(B′) is the probability that there is no strike, which can be calculated as:
P(B′)=1−P(B)=1−0.65=0.35
Now substituting the known values into the equation:
1. Calculate P(B)⋅P(A|B):
P(B)⋅P(A|B)=0.65⋅0.32=0.208
2. Calculate P(B′)⋅P(A|B′):
P(B′)⋅P(A|B′)=0.35⋅0.80=0.28
Now, add these two results together to find P(A):
P(A)=0.208+0.28=0.488
Thus, the probability that the construction job will be completed on time is:
0.488
- A: the event that the construction job is completed on time.
2. P(A|B′)=0.80 (the probability that the job is completed on time given that there is no strike).
3. P(A|B)=0.32 (the probability that the job is completed on time given that there is a strike).
P(B)⋅P(A|B)=0.65⋅0.32=0.208
P(B′)⋅P(A|B′)=0.35⋅0.80=0.28
Similar Questions
A person has undertaken a construction job. The probabilities are 0.80 that there will be a strike, 0.70 that the construction job will be completed on time if there is no strike, and 0.4 that the construction job will be completed on time if there is a strike. Determine the probability that the construction job will be completed on time.
View SolutionIf 900 persons can finish the construction of a building in 40 days, how many persons are needed to complete the construction of building in 25 days.
View Solution
Knowledge Check
A man takes the contract of construction work. The probability is 0.30, if there will be no strike. The probability that the construct work will be completed on time are 0.8 and 0.3 in cases of no strike and in case strike respectively. Find the probability that the construction work will be completed in time.
A0.34B0.56C0.64D0.45A city survey found that 47% of teenagers have a part time job. The same survey found that 30% plan to attend college. Find the probability that a teenager has a part time job.
A37/100B30/100C40/100D47/10025 men can complete a job in 30 days. After how many days should the strength of work force be increased by 50 men so that the work will be completed 23rd in of the actual time:
A15B10C18D5
In a building programme the event that all the materials will be delivered at the correct time is M, and the event that the building programme will be completed on time is F. Given that P(M)=0.8&P(M∩F)=0.65.IfP(F)=0.7, find the probability that the building program me will be completed on time if all the materials are not delivered at the correct time.
View SolutionThe number of workers and the time to complete a job is a case of direct proportion.
View SolutionThe following table shows the frequency distribution of the time required for each worker to complete a work. From the table find the mean time required to complete the job for a worker.
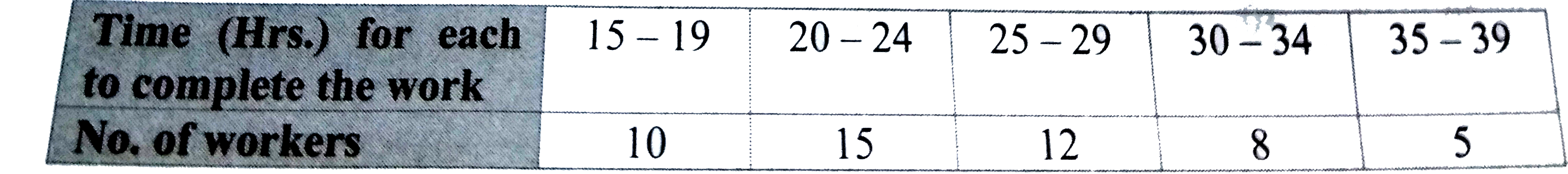
View SolutionState True or False: The Total Elapsed is the time required to complete all the jobs i.e. entire task.
View SolutionA man take 80 days to complete a job. To complete this job, 4 men, 8 women and 4 machines take 5 days. Alternatively, 4 men, 1, women and 2 machines take 10 days to complete the job. Find the time taken by a women to complete the job (in says)
View Solution
