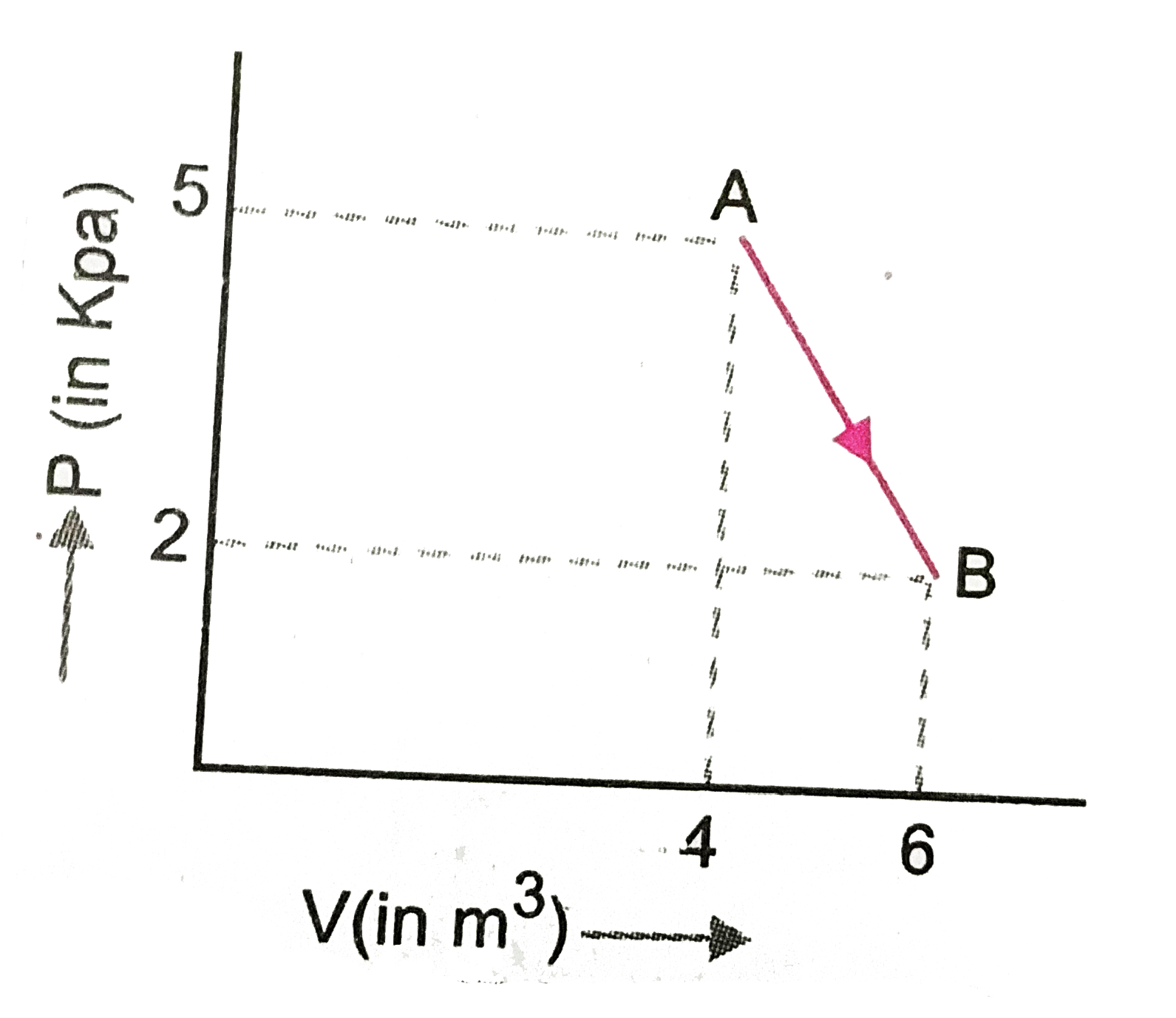
One mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in (figure). The change in internal energy of the gas during the transition is (γ=3/5)
One mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in (figure). The change in internal energy of the gas during the transition is (gamma=3//5)

A

−20KJ

B

20 J

C

−12KJ

D

20 KJ

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

Change in internal energy
ΔU=nCvΔTandT=PVnR
ΔT=T2−T1=P2V2−P1V1nR,Cv=Rγ−1
ΔU=nRγ−1(P2V2−P1V1nR)=P2V2−P1V1γ−1
=5×4−2×635−1=20−12−2/5=−82/5−20KJ

Updated on:21/07/2023
|
Class 11PHYSICSTHERMODYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • One mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure. The change in internal energy of the gas during the transition is
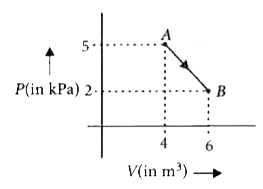    ocr_image

    A20 J
    B−12kJ
    C20 kJ
    D−20kJ

  • One mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure,
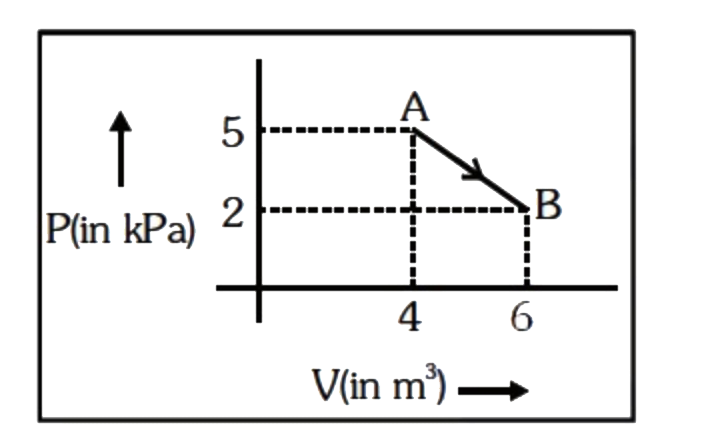
    ocr_image
    The change in internal energy of the gas during the transition is :

    A20 kJ
    B−20kJ
    C20 J
    D−20kJ

  • One mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in (figure). The change in internal energy of the gas during the transition is (γ=3/5)
    ocr_image

    A−20KJ
    B20 J
    C−12KJ
    D20 KJ