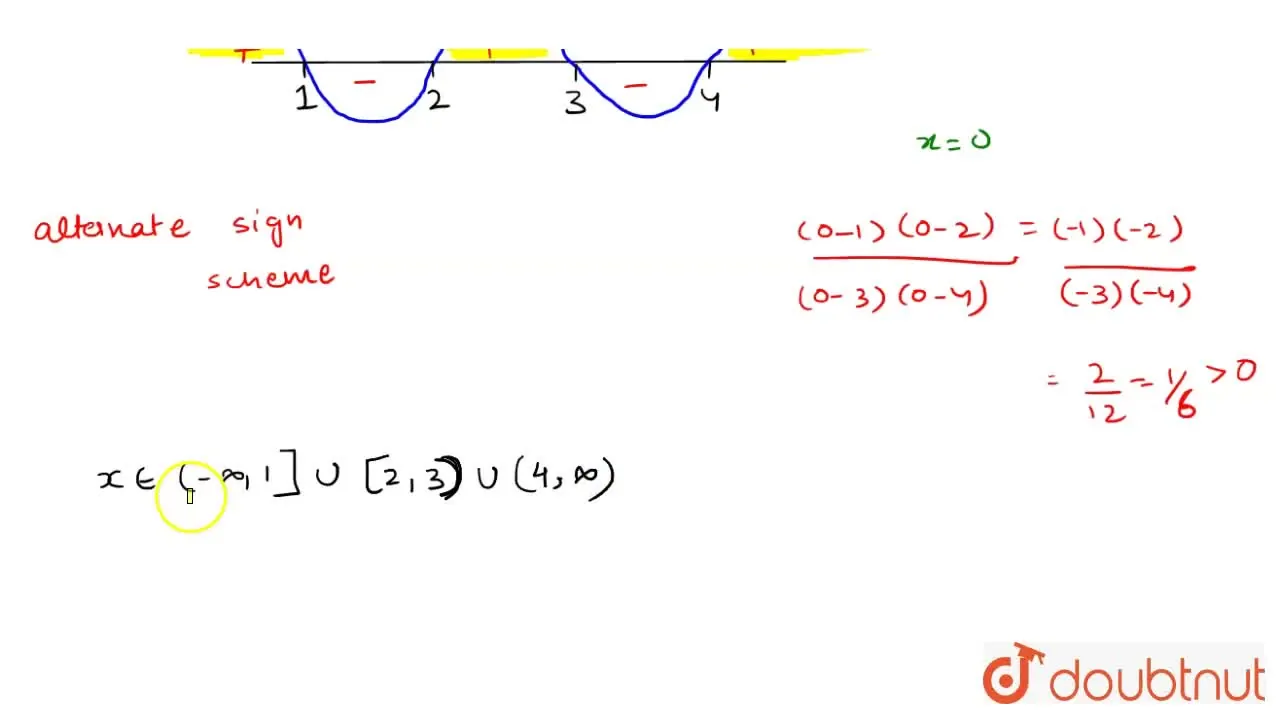
Solve (x−1)(x−2)(x−3)(x−4)≥0
The correct Answer is:X>4
Step by step video, text & image solution for Solve ((x-1)(x-2))/((x-3)(x-4))ge0 by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - LINEAR INEQUALITIESEXERCISE - LONG ANSWER TYPE QUESTIONS (Solve to the following system of inequalities and represent solution on number line:)3videos
LINEAR INEQUALITIES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - LINEAR INEQUALITIESEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS(True // False)4videos
LINEAR INEQUALITIES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - LIMITS AND DERIVATIVES EXERCISE - LONG ANSWER TYPE QUESTIONS33videos
LIMITS AND DERIVATIVES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - MATHEMATICAL REASONINGEXERCISE - SECTION-B SHORT ANSWER TYPE QUESTIONS5videos
MATHEMATICAL REASONING
Similar Questions
solve f(x)=(x−1)(2−x)(x−3)≥0.
View SolutionIf (|x|−1)(|x|−2)(|x|−3)≥0 then x lies in
View SolutionSolve the following rational in equalities
(i)(x−1)(x+2)(x−3)(x+3)<0 (ii)(1−x)3(x+2)4(x+9)2(x−8)≥0
(iii)(x2−3x+1)3(x−1)(x+2)≤0 (iv)x(2x−3x)(x2+x+1)(x−1)>0
(v)(x−1)(x−2)(x−3)(x+1)(x+2)(x+3)≤1 (vi)1<3x2−7x+8x2+1≤2View SolutionA number x is chosen at random from the set {1,2,3,4,……….,100}. Defind the event : A = the chosen number x satisfies (x−10)(x−50)(x−30)≥0, then P(A) is
View SolutionSolve the inequality (x−1)4(x−3)3(x−5)2≥0
View SolutionSolve- 12(35x+4)≥(x−6)
View SolutionSolve 2x2−x+1−1x+1−2x−1x3+1≥0.
View SolutionSove (x+2)(x2−2x+1)−4+3x−x2≥0
View SolutionFind the solution set of (x−1)(x−2)2(x+4)(x+2)(x−3)≥0
View SolutionSovle x(x+2)2(x−1)5(2x−3)(x−3)4≥0
View Solution