Solve the following systems of inequalities for all ξnR
In the first four papers each of 100 marks, Rishi got 95, 72, 73, 83 marks. If he wants an average of greater than or equal to 75 marks and less than 80 marks find the range of marks he should score in fifth paper.
The correct Answer is:He must score greater than or equal to 52 and less than 77.
To solve the problem step by step, we need to determine the range of marks Rishi should score in his fifth paper to achieve an average between 75 and 80 marks.
Step 1: Calculate the total marks obtained in the first four papers
Rishi's scores in the first four papers are:
- Paper 1: 95
- Paper 2: 72
- Paper 3: 73
- Paper 4: 83
Total marks from the first four papers:
95+72+73+83=323
Step 2: Set up the inequality for the average
Let x be the marks Rishi scores in the fifth paper. The average of the five papers should be greater than or equal to 75 and less than 80. Therefore, we can write the inequality as:
75≤323+x5<80
Step 3: Multiply the entire inequality by 5
To eliminate the fraction, we multiply all parts of the inequality by 5:
75×5≤323+x<80×5
This simplifies to:
375≤323+x<400
Step 4: Solve the inequalities
Now, we will solve each part of the inequality separately.
1. For the left part of the inequality:
375≤323+x
Subtract 323 from both sides:
375−323≤x
52≤x
So, we have:
x≥52
2. For the right part of the inequality:
323+x<400
Subtract 323 from both sides:
x<400−323
x<77
Step 5: Combine the results
Combining the results from both parts, we have:
52≤x<77
Final Answer
The range of marks Rishi should score in the fifth paper is:
x∈(52,77)
Rishi's scores in the first four papers are:
- Paper 1: 95
- Paper 2: 72
- Paper 3: 73
- Paper 4: 83
95+72+73+83=323
Let x be the marks Rishi scores in the fifth paper. The average of the five papers should be greater than or equal to 75 and less than 80. Therefore, we can write the inequality as:
75≤323+x5<80
To eliminate the fraction, we multiply all parts of the inequality by 5:
75×5≤323+x<80×5
This simplifies to:
375≤323+x<400
Now, we will solve each part of the inequality separately.
375≤323+x
Subtract 323 from both sides:
375−323≤x
52≤x
So, we have:
x≥52
323+x<400
Subtract 323 from both sides:
x<400−323
x<77
Combining the results from both parts, we have:
52≤x<77
The range of marks Rishi should score in the fifth paper is:
x∈(52,77)
Topper's Solved these Questions
- LINEAR INEQUALITIESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - LINEAR INEQUALITIESEXERCISE - LONG ANSWER TYPE QUESTIONS (Solve to the following system of inequalities and represent solution on number line:)
3 Videos
- LINEAR INEQUALITIESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - LINEAR INEQUALITIESEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS(True // False)
4 Videos
- LIMITS AND DERIVATIVES BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - LIMITS AND DERIVATIVES EXERCISE - LONG ANSWER TYPE QUESTIONS
33 Videos
- MATHEMATICAL REASONINGBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - MATHEMATICAL REASONINGEXERCISE - SECTION-B SHORT ANSWER TYPE QUESTIONS
5 Videos
Similar Questions
In the first four papers each of 100 marks, Rishi got 95,72,73,83 marks. If he wants an average of greater than or equal to 75 marks and less than 80 marks, find the range of marks he should score in the fifth paper.
View SolutionIn the first four examinations, each of 100 marks, Hamid got 94,72,72,84 marks. If a final average greater than or equal to 80 and less than 90 is needed to obtain a final grade B in a course, what range of marks on the fifth (last) examination will result Hamid in receiving grade B in course?
View Solution
Knowledge Check
A student got 20% marks and failed by 72 marks. If he scores 40% marks then he gets 8 marks more than the passing marks. Find the passing marks.
A150B152C142D160The following table shows the number of marks secured by the students of a class in a 50 marks exam.
ScoreNumber of studentsLess than or equal to 10 marks 2More than 10 marks and less then or equal to 20 marks5More than 20 marks and less then or equal to 30 marks9More than 30 marks and less then or equal to 40 marks14More than 40 marks and less then or equal to 50 marks10
How many students secured less then or equal to 30 marks in that exam ?A9B14C23D16Ravi obtained 70 and 75 marks in first two unit tests. Then, the minimum marks he should get in the third test to have an average of at least 60 marks, are
A45B35C25DNone of these
In the examination Raushan got 25% marks and failed by 64 marks. If he had got 40% marks he would have secured 32 marks more than the pass marks. Find the maximum marks in the examination.
View SolutionIn an examination, there are three papers each of 100 marks. A candidate obtained 53 marks in the first and 75 marks in the second paper. How many marks must the candidate obtain in the third paper to get an overall of 70 per cent marks?
View SolutionThe following table shows the marks of 90 students in a test of 80 marks :
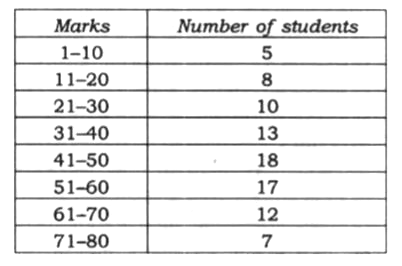
The percentage of students who have obtained less than or equal to 50% marks is
View SolutionMohan took five papers in an examination, where each paper was of 250 marks. His marks in these papers were in the ratio 6 : 8 : 10 : 12 : 15. In all papers together, Mohan obtained 70% of the total marks, Then find the number of papers in which he got more than 80% marks.
View SolutionAbhinav obtained 65 and 80 marks in first two unit test .Find the minimum marks he should get in the third test of have an average of at least 70 marks.
View Solution
